SOLUTION: Use the substitution method to solve each system and provide the coordinates. I've got most of them, but these ones I keep getting wrong. Can someone help please? (1) {{{3x-2y=3

(1) 
    

First clear them both of fractions.  To clear the first equation of
fractions multiply every term by the LCD of 2



which simplifies to

 which has no fractions.

To clear the second equation of
fractions multiply every term by LCD of 4



which simplifies to

 which has no fractions

So now the system of equations to solve is:




Rearranging the second equation like the
first equation




To make the y's cancel out, multiply the
first equation through by -2

            

which simplifies to
          

Now place the second equation directly under
this:


 

Adding term by term gives


 
--------------------
     
        
        
        

To make the x's cancel out, multiply the
second equation through by -3.








Now place this equation directly under the
first equation:

 


Adding term by term gives

 

--------------------
      
        
        
       
So the solution is (x,y) = (,0)      

============================================= 

(2) 
      

Rearrange the terms of the first equation as 
Rearrange the terms of the second equation as 

 


The x's will cancel as they are:

Add term by term:

 

-----------------
       2y=-12
      
     

Substitute -6 for y in the 1st equation:

    
 
    
        
        

So the solution is (x,y) = (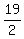,-6)

=======================================

(3)  
     

To make the r's cancel, multiply the
first equation by -3

            

          
          
Now write the second equation under this:
 
          
            
        
Add term by term:

          
           
         ------------------
             
                 
               

Substitute 4 for s in 
                 
          
            
               

So the solution is (r,s) = (3,4). So
yes it it is (3,4)!

Edwin