SOLUTION: In Triangle LMN, L=42.8° , l = 15.8cm , n=18.5cm a) Determine if the ambiguous case for this triangle. b) Solve the Triangle.

Since the side opposite the given angle is shorter than
the other given side, there are either 2 or 0 solutions.
[If there were 0 solution we will encounter an error
in the calculator, or observe that a sine cannot be 
greater than 1.]

Using the law of sines:



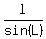Cross-multiply:



Substitute given quantities



Divide both sides by 15.8



Calculate the right side on your calculator:



Use the inverse sine feature on your calculator:

You get 52.70708059°, but that is only the possible
angle in QI where angles are acute (less than 90°).  
But the sine is also positive in QII where angles 
are obtuse (greater than 90° but less than 180°).

So the two possible angles for N are 1)  52.70708059°
and 2)  its supplement 180°-52.70708059° = 127.2929194°.

Solving the first triangle which has parts:

L=42.8° , l = 15.8cm , n=18.5cm, N=52.70708059°

And since the sum of the angles of any triangle is 180°,

M = 180°-(L+N) = 180°-(42.8°+52.70708059°) = 84.49291941°

We use the law of sines:



Multiply both sides by sin(M)



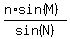Substitute known parts:



Use your calculator



So the first solution is

L=42.8° , l=15.8cm , n=18.5cm, 
N=52.70708059°, M=84.49291941°, m=12.62795038cm

Now you can solve the second triangle which has parts:

L=42.8° , l = 15.8cm , n=18.5cm, N=127.2929194° 

exactly as I solved the first triangle, only using 
N=127.2929194° instead.

Edwin