Question 1044383: if (x,y,12) is decreasing geometric sequence and (x,y,9) is arthemetic sequence then..evaluate the value of x,y and find Gn
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
if (x,y,12) is decreasing geometric sequence and (x,y,9) is arthemetic sequence then..evaluate the value of x,y and find Gn
~~~~~~~~~~~~~~~~~~~~~~
1. Since (x,y,12) is a geometric sequence, you have
 = = 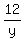 , or , or  = = 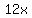 . (1)
2. Since (x,y,9) is an arithmetic sequence, you have
y - x = 9 - y, or 2y = 9 + x (2)
3. From (2), express x = 2y-9 and substitute it into (1). You will get . (1)
2. Since (x,y,9) is an arithmetic sequence, you have
y - x = 9 - y, or 2y = 9 + x (2)
3. From (2), express x = 2y-9 and substitute it into (1). You will get
 = 12*(2y-9), or = 12*(2y-9), or
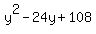 = =  .
The solutions are y = 6 and/or 18.
4. a) If y = 6, then the first progression (GP) is (3, 6, 12) and the second progression (AP) is (3, 6, 9).
b) If y = 18, then the first progression (GP) is (27, 18, 12) and the second progression (AP) is (27, 18, 9).
5. Since the GP is decreasing, it leaves only one answer: b) .
The solutions are y = 6 and/or 18.
4. a) If y = 6, then the first progression (GP) is (3, 6, 12) and the second progression (AP) is (3, 6, 9).
b) If y = 18, then the first progression (GP) is (27, 18, 12) and the second progression (AP) is (27, 18, 9).
5. Since the GP is decreasing, it leaves only one answer: b)
These two lessons in this site
- One characteristic property of arithmetic progressions
- One characteristic property of geometric progressions
helped me to quickly solve the problem.
|
|
|