|
Question 1044336: Give the coordinates of the center, foci, and covertices of the ellipse with equation 41x^2 + 16y^2 + 246x - 192y + 289 = 0.
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Give the coordinates of the center, foci, and covertices
of the ellipse with equation
41x^2 + 16y^2 + 246x - 192y + 289 = 0.
Rearrange
 Factor out coefficients of squared letters:
Factor out coefficients of squared letters:
 To complete the squares, we need to add a number to the
end of each parentheses, and to the right side:
To complete the squares, we need to add a number to the
end of each parentheses, and to the right side:
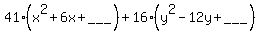   so we put a blank where we need to add numbers.
To complete the square in the first parentheses:
1. Multiply the coefficient of x by
so we put a blank where we need to add numbers.
To complete the square in the first parentheses:
1. Multiply the coefficient of x by  : :
 2. Square that result:
2. Square that result:
 3. Put that where the first blank is on the left side:
3. Put that where the first blank is on the left side:
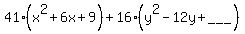   So we complete the square in the first parentheses by
adding +9 inside the first parentheses
which actually amounts to adding 41*9 or 369 to the left
side because there is a 41 in front of the parentheses, so
we must add 369 to the right side:
So we complete the square in the first parentheses by
adding +9 inside the first parentheses
which actually amounts to adding 41*9 or 369 to the left
side because there is a 41 in front of the parentheses, so
we must add 369 to the right side:
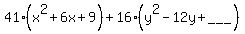  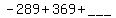 To complete the square in the second parentheses:
1. Multiply the coefficient of y by
To complete the square in the second parentheses:
1. Multiply the coefficient of y by  : :
 2. Square that result:
2. Square that result:
 3. Put that 36 in the remaining blank on the left side:
3. Put that 36 in the remaining blank on the left side:
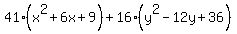  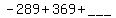 Since we complete the square in the second parentheses by adding +36
inside the second parentheses, that actually amounts to adding 16*36
or 576 to the left side because there is a 16 in front of the
parentheses, so we must add 576 to the right side, so we put 576
in the remaining blank on the right side:
Since we complete the square in the second parentheses by adding +36
inside the second parentheses, that actually amounts to adding 16*36
or 576 to the left side because there is a 16 in front of the
parentheses, so we must add 576 to the right side, so we put 576
in the remaining blank on the right side:
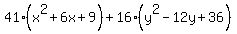   We factor both parentheses as perfect squares of binomials,
and combine the numbers on the right side:
We factor both parentheses as perfect squares of binomials,
and combine the numbers on the right side:
 Get a 1 on the right by dividing through by 656
Get a 1 on the right by dividing through by 656
 Simplify. 41 goes into 656 16 times, and 16 goes
into 656 41 times
Simplify. 41 goes into 656 16 times, and 16 goes
into 656 41 times
 Since the largest denominator is under the term in
y, the ellipse has a vertical major axis. So we
compare it to:
Since the largest denominator is under the term in
y, the ellipse has a vertical major axis. So we
compare it to:

 , ,  , ,
 so so 
 so so  Draw the major axis
Draw the major axis  units both above and below the center.
Draw the minor axis units both above and below the center.
Draw the minor axis  units both right and left of the center. units both right and left of the center.
 The vertices are
The vertices are  units above and below the center (-3,6)
So we add units above and below the center (-3,6)
So we add  to the y-coordinate of the center. So the
upper vertex is to the y-coordinate of the center. So the
upper vertex is 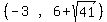 And we subtract
And we subtract  from the y-coordinate of the center. So the
upper vertex is from the y-coordinate of the center. So the
upper vertex is 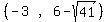 The covertices are b=3 units left and right of the center (-3,6)
So we add 3 to the x-coordinate of the center. So the
right covertex is (0,6)
And we subtract 3 from the x-coordinate of the center. So the
left covertex is (-6,6)
Sketch in the ellipse:
The covertices are b=3 units left and right of the center (-3,6)
So we add 3 to the x-coordinate of the center. So the
right covertex is (0,6)
And we subtract 3 from the x-coordinate of the center. So the
left covertex is (-6,6)
Sketch in the ellipse:
 To find the foci, we must calculate c, using the Pythagorean
relationship
To find the foci, we must calculate c, using the Pythagorean
relationship






 The foci are
The foci are  units above and below the
center (-3,6)
So we add units above and below the
center (-3,6)
So we add  to the y-coordinate of the center
So the upper focus is to the y-coordinate of the center
So the upper focus is 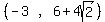 And we subtract
And we subtract  from the y-coordinate of
the center.
So the lower focus is from the y-coordinate of
the center.
So the lower focus is 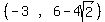 They are approximately
(-3,11.7) and (-3,0.34).
We plot the two foci:
They are approximately
(-3,11.7) and (-3,0.34).
We plot the two foci:
 Edwin
Edwin
|
|
|
| |