SOLUTION: Sakura speaks 150 words per minute on average in Hungarian, and 190words per minute on average in Polish. She once gave cooking instructions in Hungarian, followed by cleaning inst

Click here to see ALL problems on Systems-of-equations

Question 1044313: Sakura speaks 150 words per minute on average in Hungarian, and 190words per minute on average in Polish. She once gave cooking instructions in Hungarian, followed by cleaning instructions in Polish. Sakura spent 5 minutes total giving both instructions, and spoke 270 more words in Polish than in Hungarian.
How long did Sakura speak in Hungarian, and how long did she speak in Polish?
Hi! thank you so much for your help!
stuggling with a couple of these problems
Found 3 solutions by ikleyn, josgarithmetic, josmiceli:
Answer by ikleyn(52814)   (Show Source):
You can put this solution on YOUR website!
.
Sakura speaks 150 words per minute on average in Hungarian, and 190words per minute on average in Polish.
She once gave cooking instructions in Hungarian, followed by cleaning instructions in Polish.
Sakura spent 5 minutes total giving both instructions, and spoke 270 more words in Polish than in Hungarian.
How long did Sakura speak in Hungarian, and how long did she speak in Polish?
Hi! thank you so much for your help!
stuggling with a couple of these problems
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

p + h = 5, (1) (p = time in minutes speaking Polish, h = . . . Hungarian) 190*p - 150*h = 270. (2) To solve it, multiply eq. (1) by 150 (both sides) and then add to eq. (2). You will get 190p + 150p = 270 + 5*150, 340p = 1020 ---> p = 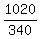= 3. Answer. 3 minutes speaking Polish and 2 minutes speaking Hungarian.

Answer by josgarithmetic(39620)   (Show Source):
You can put this solution on YOUR website!
This is a uniform-rates problem. Identify the rate, write the basic equation, and then translate the complete problem description.

Two different rates are given: for Hungarian, and for Polish. If using variables this way,
R________ for rate
w ________for count of words
t ________for count of time in minutes

then .

Analyze the problem description and setup a data table, the way you often can for most uniform rates problems.

RATE TIME WORDS HUNGARIAN 150 w POLISH 190 w+270 TOTALS 5

The actual given values are filled into the table and the one unknown variable is count of words done in Hungarian, as w. The table is still missing two data items. FILL THEM and then write the necessary equation!

Once that is done, ..., remind yourself of what questions you are supposed to answer.

Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website!
Let = minutes spent speaking in Hungarian
Let = minutes spent speaking in Polish
-----------------------------------------
(1)
(2)
-------------------------
(2)
(2)
---------------------
Multiply both sides of (1) by
and add (1) and (2)
(1)
(2)
-------------------------

and
(1)
(1)
(1)
-------------------
Sakura spent 2 min speaking in Hungarian
and 3 min speaking in Polish
-------------------------
check:
(2)
(2)
(2)
(2)
OK