SOLUTION: A metallurgist has one alloy containing 24% aluminum and another containing 70% aluminum. How many pounds of each alloy must he use to make 44 pounds of a third alloy containing 58

Take "x" pounds    of the first  alloy containing 24% aluminum.
Take (44-x) pounds of the second alloy containing 70% aluminum.

After melting and mixing these alloys you will have 44 pounds of a new alloy.

To provide a 58% content of aluminum in it, the amount "x" must satisfies this equation

0.24x + 0.7*(44-x) = 0.58*44,   or

0.24x + 30.8 - 0.7x = 25.52,   or

-0.46x = 25.52 - 30.8,

-0.46x = --5.28,

x = 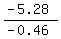 = 11.478.

So, you need to mix 11.478 pounds of the 24% alloy with 44-11.478 = 32.52 pounds of the 70% alloy.

Answer.  Metallurgist need to mix 11.478 pounds of the 24% alloy with 32.522 pounds of the 70% alloy.