Question 1044149: can you slove this inequality?
x^3-4x<0
Found 2 solutions by KMST, ikleyn:
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 
Just kidding!
There are many ways to the answer. The expected way may depend of what you have been learning in class, and teacher preference.
1) Just factor that polynomial.
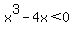
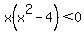
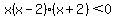
For  , ,  , and , and 
 . .
For other values of  the polynomial is either positive or negative. the polynomial is either positive or negative.
1a) You could consider the cases
 , ,  , , 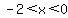 , and , and  individually. individually.
1b) You could draw 3 number lines for the factors (one for each factor) and a number line for the product;
decorate the factor number lines with "0" where the factor is zero,
"-" where the factor is negative, and "+" where it is positive:
and then figure out similar decoration for the product number line by multiplying.
Did your teacher show that way to do it in class?
1c) You could realize that
at each of the zeros the polynomial changes sign (positive to negative or vice versa), and
for  all the factors and all the factors and  . .
Either way, you realize that the polynomial is negative in the intervals
   and and 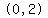 , ,
or expressed as an inequality  and and 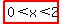 . .
1d) Yet another way is to use "test numbers" in those intervals
Doing that, you see that
for  , ,  , so , so 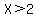 is not the right answer; is not the right answer;
for  , ,  , so , so 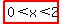 works; works;
for  , ,  , so , so 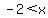 is not the right answer, and is not the right answer, and
for  , ,  , so , so  works. works.
Are there other ways to get to the answer?
2) Use a graphing calculator?
3) Use your knowledge (if any) of polynomial function behavior at the ends and at zeros of multiplicity 1.
Answer by ikleyn(52788)   (Show Source): (Show Source):
|
|
|