SOLUTION: The centre of a circle has coordinates (0,0) One end of a diameter is located at (7,-2) a) What are the coordinates of the other endpoint of this diameter? b) What is the eq

Algebra ->  Test -> SOLUTION: The centre of a circle has coordinates (0,0) One end of a diameter is located at (7,-2) a) What are the coordinates of the other endpoint of this diameter? b) What is the eq      Log On


   

Question 1044110: The centre of a circle has coordinates (0,0) One end of a diameter is located at (7,-2)
a) What are the coordinates of the other endpoint of this diameter?
b) What is the equation of the circle?
Found 3 solutions by MathLover1, solver91311, advanced_Learner:
Answer by MathLover1(20850) About Me  (Show Source):
You can put this solution on YOUR website!
(0, 0) is the midpoint of the diameter. Use the midpoint formula to determine the other end point.
0=%28x%2B7%29%2F2=>x%2B7=0=>x=-7
0=%28y%2B%28-2%29%29%2F2=>y-2=0=>y=2
the other endpoint is at (-7,2)

b)
recall standard formula for a circle:
%28x-h%29%5E2+%2B+%28y-k%29%5E2+=+r%5E2, where r being the radius , h and k are x and y coordinates of the center
since the center is at origin, h=0 and k=0 and your formula is
x%5E2+%2B+y%5E2+=+r%5E2

the length of the radius is 1%2F2 of the distance between two endpoints

r=sqrt%28+%28x1-x2%29%5E2%2B%28y1-y2%29%5E2%29%2F2
r=sqrt%28+%287-%28-7%29%29%5E2%2B%28-2-2%29%5E2%29%2F2
r=sqrt%28+%287%2B7%29%5E2%2B%28-2-2%29%5E2%29%2F2
r=sqrt%28+14%5E2%2B%28-4%29%5E2%29%2F2
r=sqrt%28+196%2B16%29%2F2
r=sqrt%28+212%29%2F2
r=sqrt%28+53%2A4%29%2F2
r=2sqrt%28+53%29%2F2
r=sqrt%28+53%29.......exact solution
so, your equation is:
x%5E2+%2B+y%5E2+=+%28sqrt%28+53%29%29%5E2
highlight%28x%5E2+%2B+y%5E2+=+53%29



Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!


The center of a circle is the midpoint of a diameter. So, given a midpoint and endpoint of a line segment, calculate the coordinates of the other endpoint using the midpoint formulas:

and



where and are the coordinates of the end points and are the coordinates of the midpoint.



is the equation of a circle with center and radius .

The radius of a circle is the distance from the center to any point on the circle. Use the distance formula to find the radius. Since the equation of the circle requires the value of the radius squared, you don't need to take the square root when using the distance formula.



where and are the coordinates of the end points of the segment for which you want to determine the length.

John

My calculator said it, I believe it, that settles it

Answer by advanced_Learner(501) About Me  (Show Source):
You can put this solution on YOUR website!
The centre of a circle has coordinates (0,0) One end of a diameter is located at (7,-2)
a) What are the coordinates of the other endpoint of this diameter?
b) What is the equation of the circle?
many ways to tackle this.
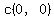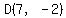
c%280%2C0%29,D%287%2C-2%29
by inspection the other end of the diameter is located at 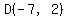D%28-7%2C2%29.
use midpoint formula to verify
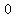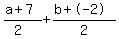
(0%2C0%29=%28a%2B7%29%2F%282%29%2B%28b%2B-2%29%2F2
means
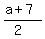%280%29=%28a%2B7%29%2F%282%29,a%2B7=0,a=-7
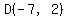
0=%28b%2B-2%29%2F2,b-2=0,b=2 therefore D%28-7%2C2%29
two ways
find the distance from end of the diamater to other end to get diameter ,divide by 2 to get radius.using (7, -2) and (-7, 2)
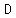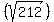
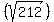
D+ = %28+sqrt+%28+212%2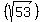9%29
D+ = %28+sqrt+%28+212%29%29
D+ = 2%28+sqrt+%28+53%29%29
half of it is the radius or 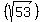R+ = %28+sqrt+%28+53%29%29
same can be found using origin and one end of the diameter to get radius.
distance from one end to the origin c(0,0) to get radius using ((0 ,0))and ((7 ,-2))
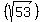
R = %28+sqrt+%28+53%29%29
the equation is
x%5E2%2By%5E2=r%5E2
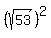x%5E2%2By%5E2=%28sqrt%2853%29%29%5E2%0D%0A%0D%0A%7B%7B%7Bx%5E2%2By%5E2=53