SOLUTION: Find the number of sides of each of the two polygons if the total number of sides of the polygons is 15 and the sum of the number of diagonals is 36

First equation is 
m + n = 15.                    (1)

The second equation is

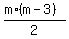 +  = 36.   (2)  ( the number of diags of an n-sided polygon is  )

Simplify and rewrite it:

m + n = 15,                   (1')
n^2 - 3n + m^2 - 3m = 72.     (2')

Simplify and rewrite it one more time. In the second eqn. use m+n = 15:

m + n = 15,                   (1'')
n^2 + m^2 = 72+3*15.          (2'')
 
or

m + n = 15,                   (1''')
n^2 + m^2 = 117.              (2''')

Solve by the substitution method.

Answer.  1) n = 6, m = 9.   2) n = 9, m= 6.