Question 1043933: out of 2n+1 students, n are to be awarded scholarship. number of ways in which at least one student gets scholarship is 63. find out how many students are recieving the scholarship.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I have been struggling to understand what the wording of the question means.
There are  students applying for those scholarships. students applying for those scholarships.
Are those  scholarships distinguishable from each other? scholarships distinguishable from each other?
Does "at least one student gets scholarship" mean  ? ?
Does the wording mean that maybe not all the  scholarships will be awarded, but at least scholarships will be awarded, but at least  will be awarded? will be awarded?
The meaning of the wording has to allow the existence of  different possible outcomes. I could think of only one way to make that wording work. different possible outcomes. I could think of only one way to make that wording work.
Let's say the scholarships are indistinguishable from each other, and at least  , but at most , but at most  will be awarded: will be awarded:
If just  is awarded, that is combinations of is awarded, that is combinations of 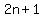 taken taken  at a time, at a time,
and that is obviously 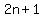 ways, ways,
because the single scholarship could be awarded to any of the 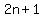 students. students.
How many different ways could it happen that exactly  scholarship is awarded? scholarship is awarded?
That is combinations of 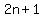 taken taken  at a time, at a time,
and that is  . .
Similarly we would get to a number for the case that exactly  , ,  , ,  , ,  scholarships could be awarded. scholarships could be awarded.
There are 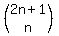 = =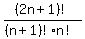 possible different sets of possible different sets of  students that could be chosen to receive scholarships out of a pool of students that could be chosen to receive scholarships out of a pool of 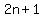 applicants. applicants.
Finding  so that the total of possible different sets of so that the total of possible different sets of
 , ,  , ,  , ,  , or , or  scholarship recipients adds up to scholarship recipients adds up to  appears complicated, appears complicated,
but the fact that  is a relatively small number makes it easy. is a relatively small number makes it easy.
For  , ,  and there are and there are
 possible different sets of possible different sets of  students that can be chosen from students that can be chosen from  applicants. applicants.
Since 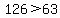 , we need to choose a smaller , we need to choose a smaller  . .
It so happens that  works. works.
For  , ,  and from a pool of and from a pool of  students, there can be students, there can be
 possible different sets of possible different sets of  students: students:
 possible different sets of possible different sets of  students, and students, and
 sets of sets of  student student
that can be chosen to receive scholarships.
All in all there are  possible sets of possible sets of  , ,  , or , or  students that can be chosen to receive scholarships out of a total of students that can be chosen to receive scholarships out of a total of  student applicants. student applicants.
|
|
|