Question 1043924: find the point of intersection of x^2+y^2=25,
x^2/18+ y^2/32=1
Found 2 solutions by ikleyn, solver91311:
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
find the point of intersection of x^2+y^2=25,
x^2/18+ y^2/32=1
~~~~~~~~~~~~~~~~~~
 = 25, (1) = 25, (1)
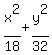 = 1. (2)
Multiply (2) by 18 (both sides). You will get = 1. (2)
Multiply (2) by 18 (both sides). You will get
 = 25, (1') = 25, (1')
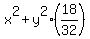 = 18, (2')
or equivalently = 18, (2')
or equivalently
 = 25, (1'') = 25, (1'')
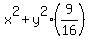 = 18. (2'')
Distract (2'') from (1''). You will get = 18. (2'')
Distract (2'') from (1''). You will get
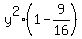 = 25 - 18, or = 25 - 18, or  = 7, or = 7, or  = 16.
Hence, y = +/- 4.
Then from (1) x = +/-3.
Answer. There are four solution and, respectively, four intersection points:
(x,y) = (3,4), (3,-4), (-3,-4), (-3, 4). = 16.
Hence, y = +/- 4.
Then from (1) x = +/-3.
Answer. There are four solution and, respectively, four intersection points:
(x,y) = (3,4), (3,-4), (-3,-4), (-3, 4).
Answer by solver91311(24713)   (Show Source): (Show Source):
|
|
|