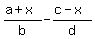
SOLUTION: {{{(a + x)/b - (c - x)/d }}}{{{""=""}}}{{{ a/b}}} I understand more but not totally. I have been out of school 40 yrs. and trying to relearn math/algebra on my own. The qu

  
OK, here is a walk-through step-by step.  Notice there are
three letters a,b, and x.  Usually, letters nearer the first of
the alphabet are considered to represent constants.  Letters 
nearer the end of the alphabet are usually variables, and they 
are usually the ones to solve an equation for, unless you are
told otherwise.  So we solve for x.



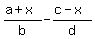Look at all the denominators. They are
b and d.  Multiply them together and get b*d.

So the least or lowest common denominator is b*d.

Put both sides in parentheses and multiply both 
sides by b*d:



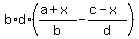Distribute the b*d on the left to remove the parentheses:



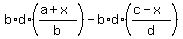Cancel the b's in the first term on the left side.
Cancel the d's in the second term on the left side.
Cancel the b's on the right side.





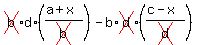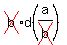
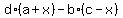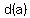Distribute to remove the parentheses on the left.
Be careful when you distribute the -b* to notice
that it has a - sign before it.  So when you
distribute, notice carefully that the x also has 
a - sign before it, so when you multiply the
-b by the -x you get a +b*x, not a -b*x.

Write the right side as d*a:



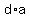Subtract d*a from both sides eliminates if from both sides,
and leaves a zero on the right side:



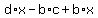We want to get all the terms containing x on the left and only
terms that do not contain x on the right.  So we add +b*c to
both sides to get rid of the -b*c term on the left that does not
contain x:



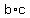Now we factor out the x on the left (That's the reverse of the
distributive principle, putting in parentheses instead of
removing parentheses:



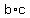Divide both sides by (d+b)



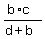Cancel the (d+b)'s on the left



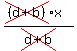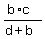And we end up with



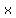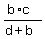Edwin