SOLUTION: x^2+y^2+z^2=2(x+z-1) then the value of x^3+y^3+z^3

If   = 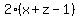,  then

 = ,

 = ,

 = .

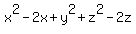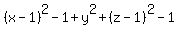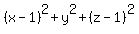We have the sum of squares of three real numbers equal to zero.
Hence, each of the three numbers is equal to zero:

x-1 = 0,  y = 0  and  z-1 = 0.

In other words, x = 1, y = 0, z = 1.

Now  = -2.