Question 1043668: A football is kicked 70cm from the ground and follows a parabolic path. When it was 4m from where it was kicked, its height was 5.7m and it lands 10m from where it was kicked. Find the maximum height reached by the ball, by first forming an equation.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! A football is kicked 70cm from the ground and follows a parabolic path.
When it was 4m from where it was kicked, its height was 5.7m and it lands 10m from where it was kicked.
Find the maximum height reached by the ball, by first forming an equation.
:
Change 70cm to .7 meters
:
Using the form ax^2 + bx + c = y
Form three x/y points
0,.7; the point it is kicked (c=.7)
4, 5.7
10, 0; the point where it lands
:
Write an equation for the 2nd and 3rd points
4^2a + 4b + .7 = 5.7
16a + 4b = 5
and
10^2a + 10b + .7 = 0
100a + 10b = -.7
Use elimination, multiply the 1st equation by 10, 2nd equation by 4
160a + 40b = 50
400a + 40b = -2.8
------------------ subtraction eliminates b, find a
-240a = 52.8
a = 52.8/-240
a = -.22
Find b, a=-.22
16(-.22) + 4b = 5
-3.52 + 4b = 5
4b = 5 + 3.52
4b = 8.52
b = 8.52/4
b = 2.13
:
The equation: y = -.22x^2 + 2.13x + .7
:
looks like this

"Find the maximum height reached by the ball"
Find the axis of symmetry, x = -b/(2a)
x = 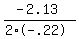
x = 4.84
Find the max height when x=4.84
y = -.22(4.84^2) + 2.13(4.84) + .7
y = -5.155 + 10.31 + .7
y = 5.8556 meters max height (green line)
|
|
|