Question 1043659: Ref. 1043615:
I still don't understand. Never mind. Sorry for asking the question.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! I think this is the answer you needed all along.
The original answer started by finding an expression for  that did not involve that did not involve  , ,
 , ,
and along the way you had the equation  or or  . .
Just substitute the expression 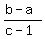 for for  into into  , ,
and you get  . .
The solution to the system of equations is
 . .
You do not need to substitute the expression 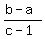 for for  into "one of the original equations". into "one of the original equations".
Substituting into  is a valid, easier option. is a valid, easier option.
You do not have to worry about he constants (or variables)  , ,  , and , and  . .
APOLOGY:
I apologize for not taking the time earlier to give you the clear answer you needed.
What the original answer may have tried to do is showing you that there are many different ways to solve a system of linear equations.
What you needed was an easy and clear way to the solution.
EXTRA (optional reading):
In solving systems of 2 equations with 2 variables,
each step changes one equation at a time,
but you always have two (hopefully independent) equations.
I like to think of a solution as
 ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> . .
Each system is "equivalent to" (has exactly the same solutions as) the other systems.
It is not necessary to write all that,
but thinking of it that way helps you keep track of what 2 equations you are working with, so you do not end up with 2 versions of the same equation.
|
|
|