.
Please help me solve this question x^2+y^2+z^2=2(x+z-1)then the value of x^2+y^2+z^2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
If  =
= 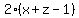 , then
, then
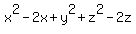 =
=  ,
,
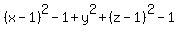 =
=  ,
,
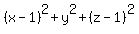 =
=  .
We have the sum of squares of three real numbers equal to zero.
Hence, each of the three numbers is equal to zero:
x-1 = 0, y = 0 and z-1 = 0.
In other words, x = 1, y = 0, z = 1.
Now
.
We have the sum of squares of three real numbers equal to zero.
Hence, each of the three numbers is equal to zero:
x-1 = 0, y = 0 and z-1 = 0.
In other words, x = 1, y = 0, z = 1.
Now  = 2.
= 2.
Solved.