Question 1043572: 1. A ship leaves a port and sails for 4 hours on a course of 78° at 18 knots. Then the ship changes it's course to 128° and sails for 6 hours at 16 knots. Find 10 hours after leaving the port:
*the distance of ship from the part
*the bearing of the ship from the port
*the bearing from the ship to the port.
2. A ship is sailing due west when a light is observed with heading 297°50' from the ship. After the ship has travelled 2250 feet, the light heads 311°55' from the ship. If the course is continued, how close will the ship approach the light?
Please provide illustrations so I could study it. Thank you.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1. I had to look up the definition of course, heading, and bearing,
and what I found is some confusion.
In most sources They were defined as the angle from North to the direction the ship is aiming for, or pointing to,
measured clockwise from North.
I am sticking to that, but I believe that for the first problem, it does not matter how you measure the angle, as long as it is done consistently.
 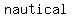 
 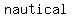  . .
The situation can be sketched like this:

The right triangles with a red hypotenuse of length 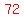 have legs measuring have legs measuring
 (rounded to 5 decimal places) and (rounded to 5 decimal places) and
 (rounded to 5 decimal places) . (rounded to 5 decimal places) .
At  hours the ship was about 70 nautical miles East, and 15 miles North of the port. hours the ship was about 70 nautical miles East, and 15 miles North of the port.
The legs of the right triangles with a green hypotenuse of length  are such that are such that
 (rounded to 5 decimal places) and (rounded to 5 decimal places) and
 (rounded to 5 decimal places) . (rounded to 5 decimal places) .
After  hours the ship was about 76 nautical miles further East, and 59 miles South from its position at hours the ship was about 76 nautical miles further East, and 59 miles South from its position at  hours. hours.
Considering only the start and end positions, we have
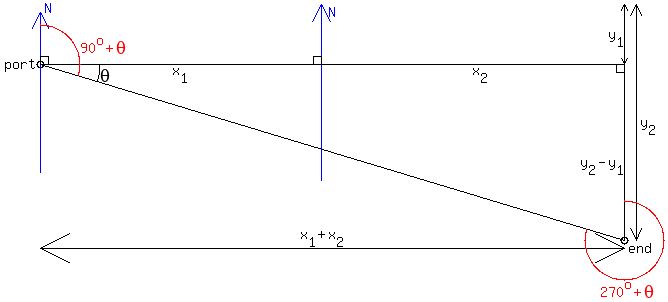
We have one right triangle, and we know the legs, so we can find
the hypotenuse, and
angle  . .
The lengths of the legs are approximately
 and and  ; ;
 ---> ---> . .
So,
the distance to the ship from the port is  nautical miles, nautical miles,
the bearing of the ship from the port is  , and , and
the bearing from the ship to the port is
 . .
2. The ship is going West.
When the ship reaches point  it records the bearing/heading of the light, it records the bearing/heading of the light,
and it does it again, 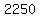 feet further, at point feet further, at point  . .
If the course is continued,  feet further, the ship will reach point feet further, the ship will reach point  , ,
where it is at a distance of  feet from the light, feet from the light,
as close to the light as its westward trajectory would take it.

We have two right triangles:  and and 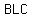 . .
For triangle  , a leg measuring , a leg measuring  feet is opposed to an angle measuring feet is opposed to an angle measuring    , ,
while leg measuring 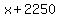 feet is adjacent to the same angle. feet is adjacent to the same angle.
So,  . .
For triangle 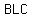 , a leg measuring , a leg measuring  feet is opposed to an angle measuring feet is opposed to an angle measuring 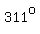   , ,
while leg measuring  feet is adjacent to the same angle. feet is adjacent to the same angle.
So,  . .
Dividing one equation vby the other, we get
 ,which can be solved for ,which can be solved for  . .
Then, we can use  <---> <---> to find to find  . .
Solving:






 , ,
and finally

That calculates as approximately
 feet. feet.
|
|
|