Question 1043527: during a 3 years boom, a government experienced a budget surplus of 15 million dollars per year. a economist predicts that annual revenue will drop to 40 million dollars below current levels and remain at that level for the next 5 years. by how much must the government reduce expenditures yearly to maintain a balanced budget over this period?
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! WHAT WE KNOW:
 = government annual expenditure during each year of the 3-year boom (in millions of dollars).
 = government annual revenue during each year of the 3-year boom (in millions of dollars).
They tell us that  , so  .
That means that by the end of the 3-year boom,
The government has a nice  million dollars surplus saved for a rainy day.
 = the economist-predicted annual revenue for the next 5 years (in millions of dollars).
WHAT WE THINK:
Let us plan what the expenditure will be for the next 5 years.
(We will make it the same amount each year).
Obviously the annual expenditure needs to be less for the next 5 years.
Lets budget the smaller amount  to be the annual expenditure for each of the next 5 (lean) years.
Over the next 5 (lean) years the annual expenditure will be million dollars,
and the total expenditure (in millions of dollars) will be  .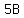
At the same time (in millions of dollars), the annual revenue will be  ,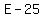
and the total revenue will be  .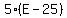
To have a balanced budget, the total revenue for the 5 lean years plus the saving from the boom years must equal the total expenditure for the 5 lean years.
So, our new equation is
 .
SOLVING THE EQUATION:
 .
That is (in millions of dollars) the difference between what the government was spending each year during the boom, ,
and what the government can afford to spend, , during each of the next 5 lean years.
Over the next 5 lean years the government's annual expenditure must be  ,
 million dollars less than it was during the boom years.
|
|
|
