Question 1043518: a ladder 6m long leans against a vertical wall so that it makes an angle of 60degrees with the wall
.calculate the distance of the foot of the ladder from the wall
Found 2 solutions by Boreal, MathTherapy:
Answer by Boreal(15235)   (Show Source):
You can put this solution on YOUR website! Drawing it helps.
|\
The ladder's angle with the wall is where the two lines are closest, as I interpret the question.
That angle is 60 degrees, and the ladder is the hypotenuse of a 30-60-90 triangle. The ladder is 6 feet long, the distance it is up the wall is half of that or 3 feet, and the distance of the foot of the ladder from the wall is sqrt(3^2+ x^2)=36, or 6^2
sqrt(9+x^2)=sqrt(36)
x^2 must equal 27, or 3 sqrt (3).
================
Also, a 30-60-90 triangle has 1-sqrt(3)-2 ratio, so if the hypotenuse is 3 times that, or 6, the longer leg must be 3 sqrt (3)feet, or 5.2 feet approximately.
Answer by MathTherapy(10557)  (Show Source):
You can put this solution on YOUR website!
a ladder 6m long leans against a vertical wall so that it makes an angle of 60degrees with the wall
.calculate the distance of the foot of the ladder from the wall
If the hypotenuse (H) of a 30-60-90 triangle is known, its longer leg is calculated as: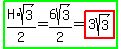 
|
|
|
