SOLUTION: The interior angles of a convex polygon form arithmetic progression with common difference 4° .Determine the sides of the polygon if its largest interior angle is 172°.

Algebra ->  Sequences-and-series -> SOLUTION: The interior angles of a convex polygon form arithmetic progression with common difference 4° .Determine the sides of the polygon if its largest interior angle is 172°.      Log On


   

Question 1043390: The interior angles of a convex polygon form arithmetic progression with common difference 4° .Determine the sides of the polygon if its largest interior angle is 172°.
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
The sum of the measures of the exterior angles of a polygon is always 360%5Eo .
That is simpler and easier to see and remember than anything about interior angles.
Each exterior angle is supplementary to the adjacent interior angle,
so the measures (in degrees) of the exterior angles also form an arithmetic progression.
Starting from the smallest exterior angle, the terms of that progression are
a%5B1%5D=180-172=8 ,
a%5B2%5D=8%2B4=12 ,
a%5B3%5D=8%2B2%2A4=16 ,
and so on, up to
a%5Bn%5D=8%2B4%28n-1%29
The sum of the first n terms of an arithmetic progression is
S%5Bn%5D=n%28a%5B1%5D%2Ba%5Bn%5D%29%2F2 .
In this case, S%5Bn%5D=n%288%2B8%2B4%28n-1%29%29%2F2 ,
and it equals 360 ,
because the sum of the measures of the exterior angles of any polygon is 360%5Eo .
So,
n%288%2B8%2B4%28n-1%29%29%2F2=360
n%2816%2B4n-4%29%2F2=360
n%2812%2B4n%29=360%2A2
12n%2B4n%5E2=720
12n%2B4n%5E2-720=0
3n%2Bn%5E2-180=0
n%5E2%2B3n-180=0
%28n-12%29%28n%2B15%29=0
highlight%28n=12%29 .
The number of sides of the polygon is highlight%2812%29 .

NOTEs:
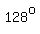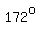The problem does not ask for the measures of any other interior angles, but they range from 128%5Eo to 172%5Eo .
We cannot find what the lengths of the sides are,
because there are many different polygons with those same angle measures.
The possibilities are endless.
Here is what one of them looks like: