Question 1043332: Determine the center,foci,vertices,and covertices of the ellipse with the given equation:
9x^2+16y^2-126x+64y=71
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 


Thge expressions in brackets remindme of some squares:
 , so , so  , and , and
 , so , so  . .
Adding 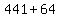 to both sides of the equal sign in the original equation, we have to both sides of the equal sign in the original equation, we have




Dividing both sides of the equal sign in the equation above by  , we have , we have


Dividing both sides of the equal sign in the equation above by  , we have , we have
 , or , or  . .
That is the equation of an ellipse centered at 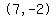 , ,
the point with  . .
The semi-major axis length is  , and , and
semi-minor axis length is  . .
The  is dividing the term with is dividing the term with  , ,
so the major axis is parallel to the x-axis,
and since the center has  , ,
the major axis is the line  . .
On that major axis, are the vertices and foci.
The minor axis is parallel to the y-axis,
and since the center has  , ,
the major axis is the line  . .
We know that the focal distance of an ellipse,  , can be found as , can be found as
 , so in this case , so in this case
 . An approximate value is . An approximate value is  . .
The locations of the foci are on the major axis,
at a distance  to either side of the center, to either side of the center,
so one the coordinates of the foci are
 , or about , or about 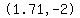 for one focus, for one focus,
and  , or about , or about 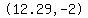 for the other focus. for the other focus.
Similarly, the vertices are on the major axis,
at a distance  to either side of the center, to either side of the center,
so one the coordinates of the vertices are
 , ,
and  . .
The covertices are on the minor axis,
at a distance  to either side of the center, to either side of the center,
so one the coordinates of the vertices are
 , ,
and  . .
The ellipse with axes and foci looks like this:
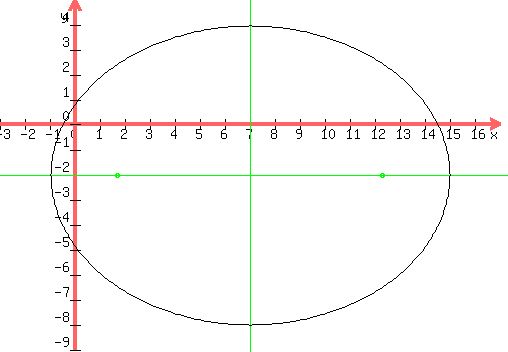
|
|
|