SOLUTION: The position vector of OP, OQ and OR is <0,0,0>, <1,2,3> and <2,1,-1> respectively. Find i) the area of the triangle PQR ii) the projection of QR and OR iii) the direction angle

Algebra ->  Vectors -> SOLUTION: The position vector of OP, OQ and OR is <0,0,0>, <1,2,3> and <2,1,-1> respectively. Find i) the area of the triangle PQR ii) the projection of QR and OR iii) the direction angle      Log On


   

Question 1043241: The position vector of OP, OQ and OR is <0,0,0>, <1,2,3> and <2,1,-1> respectively. Find
i) the area of the triangle PQR
ii) the projection of QR and OR
iii) the direction angles of vector QR
Answer by Edwin McCravy(20065) About Me  (Show Source):
You can put this solution on YOUR website!
The position vector of OP, OQ and OR is <0,0,0>, <1,2,3> and <2,1,-1> respectively. Find
i) the area of the triangle PQR
The cross product is the area of the parallelogram,
and so the area of the triangle is half that.

 

The area is ∥OQ×OR∥/2 = expr%281%2F2%29abs%28abs%28matrix%283%2C3%2Ci%2Cj%2Ck%2C1%2C2%2C3%2C2%2C1%2C-1%29%29%29 = ∥-5i+7j-3k∥/2 = sqrt%28%28-5%29%5E2%2B%287%29%5E2%2B%28-3%29%5E2%29%2F2=sqrt%2811025%29%2F2=105%2F2+=+52.5 

We find the magnitude of vectors OQ and OR

∥OQ∥ = sqrt%281%5E2%2B2%5E2%2B3%5E2%29=sqrt%2814%29

∥OR∥ = sqrt%282%5E2%2B1%5E2%2B%28-1%29%5E2%29=sqrt%286%29

-----------------------

ii) the projection of QR and OR

I think you meant "onto", not "and".

the projection of QR onto OR is given by

            OQ•OR
projOROQ  = ————— OR 
            ∥OR∥²

                          
OQ•OR = <1,2,3>•<2,1,-1> = (1)(2)+(2)(1)+(3)(-1) = 1

∥OR∥² = 2²+1²+(-1)² = 4+1+1 = 6

So,

projOROQ = 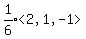expr%281%2F6%29%2A%22%3C2%2C1%2C-1%3E%22

Edwin