Question 1043225: Find the center,foci,vertices and covertices of the ellipse with the given equation.
9x^2+16y^2-126x+64y=71
Answer by ikleyn(52790)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find the center,foci,vertices and covertices of the ellipse with the given equation.
9x^2+16y^2-126x+64y=71
~~~~~~~~~~~~~~~~~~~~~~~~~~~
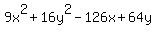 = =  ---> --->
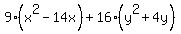 = =  ---> --->
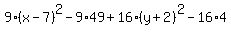 = = 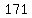 , ,
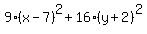 = = 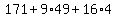 , ,
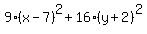 = = 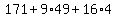 , ,
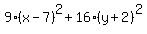 = =  , ( <--- next divide both sides by 676 = , ( <--- next divide both sides by 676 = 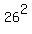 ) )
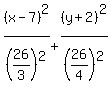 = 1, or = 1, or
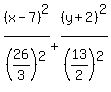 = 1.
The center of the ellipse is the point (7,-2).
The semi-major axis is a = = 1.
The center of the ellipse is the point (7,-2).
The semi-major axis is a = 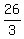 .
The semi-minor axis is b = .
The semi-minor axis is b = 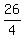 = 13/2. (Notice that a > b. The major axis is horizontal, and the ellipse is wider than tall).
Two vertices in horizontal directions are ( = 13/2. (Notice that a > b. The major axis is horizontal, and the ellipse is wider than tall).
Two vertices in horizontal directions are (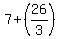 , , ) and ( ) and (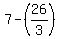 , , ).
Two vertices in vertical directions are ( ).
Two vertices in vertical directions are ( , ,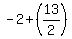 ) and ( ) and ( , , ).
The linear eccentricity is c = ).
The linear eccentricity is c = 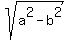 = = 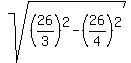 = = 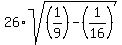 = = 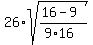 = =  = =  .
The foci are ( .
The foci are ( , , ) and ( ) and (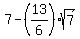 , , ). ).
See the lesson
- Ellipse definition, canonical equation, characteristic points and elements
in this site.
|
|
|