Question 1043164: A certain number of two digits is equal to five times the sum of the digits. Three times the larger digit exceeds three times the smaller by three. Find the number.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  = the larger digit = the larger digit
 = the smaller digit = the smaller digit
"Three times the larger digit exceeds three times the smaller by three" translates as
 <--> <--> <--> <--> . .
That narrows the possibilities to
10, 12, 21, 23, 32, 34, 43, 45, 54, 56, 65, 67, 76, 78, 87, 89, and 98.
What other clue do we have?
 = the tens digit = the tens digit
 = the ones digit = the ones digit
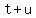 = the sum of the digits = the sum of the digits
 = the value of the number = the value of the number
The "number of two digits is equal to five times the sum of the digits"
translates into the equation
 <--> <--> <--> <--> <--> <--> <--> <--> . .
Maybe by now you realize that the number is  . .
Otherwise,  tells you that tells you that  is the smaller digit, so is the smaller digit, so  . .
 ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> ---> --->
|
|
|