Question 1043084: Sketch a graph of the polar equation, and express the equation in rectangular coordinates.
θ=-pi/2
Found 3 solutions by Edwin McCravy, ikleyn, robertb:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
   This is one that you can't use the usual formulas
to convert with. You must understand how
polar graphs work. I'll show you what you must
do when the formulas won't work:
There is no "r" in this equation, however
you could think of it as having the term 0r,
like this
This is one that you can't use the usual formulas
to convert with. You must understand how
polar graphs work. I'll show you what you must
do when the formulas won't work:
There is no "r" in this equation, however
you could think of it as having the term 0r,
like this
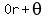   Then you can get a few polar points
r | θ
---------
1 | -π/2 (r,θ) = (1,-π/2)
2 | -π/2 (r,θ) = (2,-π/2)
3 | -π/2 (r,θ) = (3,-π/2)
-1 | -π/2 (r,θ) = (-1,-π/2)
-2 | -π/2 (r,θ) = (-2,-π/2)
-3 | -π/2 (r,θ) = (-3,-π/2)
The polar point (r,θ) means to swing a radius line around through the
angle θ, counter-clockwise if θ is positive and clockwise if
θ is negative. Then go out on that radius line as many units as
the value of r in that direction. If the value of r is
positive, you go out away from the origin (or pole). If the
value of r is negative you go backward through the origin
or pole.
Using polar graph "spider-web" paper, this is how you plot the
polar point (r,θ) = (2,-π/2).
Starting for the "east" (right side of the horizontal,
swing around through π/2 radians or 90° CLOCKWISE
since θ is NEGATIVE, indicated by the red arc,
then go out 2 units, along the red line, and plot a point.
Normally we don't show the red arc or the red line to keep
from cluttering up the graph, but I'll do it for this
illustration:
Then you can get a few polar points
r | θ
---------
1 | -π/2 (r,θ) = (1,-π/2)
2 | -π/2 (r,θ) = (2,-π/2)
3 | -π/2 (r,θ) = (3,-π/2)
-1 | -π/2 (r,θ) = (-1,-π/2)
-2 | -π/2 (r,θ) = (-2,-π/2)
-3 | -π/2 (r,θ) = (-3,-π/2)
The polar point (r,θ) means to swing a radius line around through the
angle θ, counter-clockwise if θ is positive and clockwise if
θ is negative. Then go out on that radius line as many units as
the value of r in that direction. If the value of r is
positive, you go out away from the origin (or pole). If the
value of r is negative you go backward through the origin
or pole.
Using polar graph "spider-web" paper, this is how you plot the
polar point (r,θ) = (2,-π/2).
Starting for the "east" (right side of the horizontal,
swing around through π/2 radians or 90° CLOCKWISE
since θ is NEGATIVE, indicated by the red arc,
then go out 2 units, along the red line, and plot a point.
Normally we don't show the red arc or the red line to keep
from cluttering up the graph, but I'll do it for this
illustration:
 ----
Using polar graph paper, this is how you plot the polar point
(r,θ) = (-3,-π/2).
Starting again for the "east" (right side of the horizontal,
swing around as before through π/2 radians or 90° CLOCKWISE
since θ is NEGATIVE, indicated by the red arc,
but this time how you go out is different. You go out 3 units,
but this time BACKWARDS through the origin along the red line,
which goes BACKWARDS through the origin and plot a point. That's
because the value of r is NEGATIVE. Like this:
----
Using polar graph paper, this is how you plot the polar point
(r,θ) = (-3,-π/2).
Starting again for the "east" (right side of the horizontal,
swing around as before through π/2 radians or 90° CLOCKWISE
since θ is NEGATIVE, indicated by the red arc,
but this time how you go out is different. You go out 3 units,
but this time BACKWARDS through the origin along the red line,
which goes BACKWARDS through the origin and plot a point. That's
because the value of r is NEGATIVE. Like this:
 When all the points are plotted we have this:
and when we connect all those points we have this vertical
line:
When all the points are plotted we have this:
and when we connect all those points we have this vertical
line:
 Now if we superimpose rectangular graph paper
on the "spider-web" graph paper, we get this:
Now if we superimpose rectangular graph paper
on the "spider-web" graph paper, we get this:
 As you see, the graph is the line which is the y-axis.
And the rectangular equation of the y-axis is
x = 0 <-- that's the rectangular equation for
As you see, the graph is the line which is the y-axis.
And the rectangular equation of the y-axis is
x = 0 <-- that's the rectangular equation for    If you need to ask me any questions about this, feel free
to ask them in the thank-you note form below. I'll get back
to you by email. (no charge ever. I do this as a hobby).
Edwin
If you need to ask me any questions about this, feel free
to ask them in the thank-you note form below. I'll get back
to you by email. (no charge ever. I do this as a hobby).
Edwin
Answer by ikleyn(52887)   (Show Source): (Show Source):
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! To this "tutor" "ikleyn": Go back to school. At the minimum, there is such a thing as Internet. Here are some references for you.
https://cosmolearning.org/video-lectures/graphing-polar-equations-r25-thetapi3/
https://mathway.com/popular-problems/Precalculus/407122
http://cims.nyu.edu/~kiryl/Precalculus/Section_8.2-Graphs%20of%20Polar%20Equations/Graphs%20of%20Polar%20Equations.pdf
And please DO NOT say those graphs look the way they do because the values of  are positive! are positive!
--------------------------------------------------------------------------
If the polar equation is devoid of the other variable, it means that the absent variable is free to take on ANY real value. The polar
coordinates (r, ) imply that, if ) imply that, if  , then , then 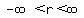 , and hence the graph is the entire , and hence the graph is the entire 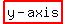 . In rectangular coordinates, it would be . In rectangular coordinates, it would be  . .
(This is much like in rectangular coordinates, where, if you have, for example, x = 5, then the graph is the vertical line with x-intercept
(5,0), meaning, y was free to vary over all real numbers.)
|
|
|