.
Tom the cat is brushing up his Math skills. He has a bag containing N balls of different colors.
Now Tom can randomly pick any even number of balls from the bag. Tom wants to find out the sum of all such combinations
of balls that he can pull out from the bag. Given he can pull out at max K balls in one pick.
Input Format:
First line contains two space separated numbers N and K
Output Format:
The output is the sum of all the combinations of balls he can pull out modulo 10^9+7 i.e. (1000000007)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This writing doesn't make sense.
Besides of it, it seems that formulations of two different problems merged mistakenly in one post here.
Actually, there is a beautiful problem close to this formulation.
But it should be cleaned/rectified and reformulated.
Let me do it below.
Tom the cat is brushing up his Math skills. He has a bag containing N balls of different colors. (Which means that the balls are distinguishable).
Let N is >= 2.
Now Tom can randomly pick any even number of balls from the bag. Tom wants to find out the 
number
of all such combinations of balls that he can pull out from the bag.
OK. Let "N" be the number of the balls in the bag.
Then Tom wants to find the number 
, summation over all even m from 0 to N (from 0 to the largest even number lesser or equal to N).
For the solution, let us call this sum as
= , summation over all even m from 0 to N (from 0 to the largest even number lesser or equal to N).
(index "e" is the first letter of the word "even").
Also, let us consider another sum,
= 
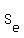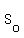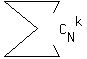, summation over all odd k from 0 to N (from zero to the largest odd number lesser or equal to N).
(index "o" is the first letter of the word "odd").
Then these two equalities are true:
1) + = 
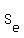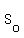, (1) and
2) 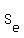= 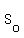. (2)
Equality (1) is true, because its left side is the sum of all binomial coefficients of the binomial expansion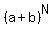 
.
Then (1) is well known property of the sum of the binomial coefficients of the binomial expansion
(see the lesson The Pascal's triangle in this site).
The property (2) is also well known. It is read as "the alternate sum of the binomial coefficients is equal to zero"
and in this form it is also proved in the referred lesson.
Fantastic! Now from (1) and (2) we have = =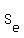 
.
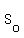This is the solution, the result and the answer for the curious Tom the cat,
and this is the solution of the problem: The number under the question is equal to .
Isn't it a beautiful problem / solution / result ?
