.
How to Solve 2^x . 3^y=5^y-x,10^x+y=2??
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
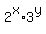 =
= 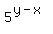 , (1)
, (1)
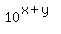 =
=  (2)
is equivalent to
x*ln(2) + y*ln(3) = (y-x)*ln(5), (1')
(x+y)*ln(10) = ln(2). (2')
It is a system of two linear equations in two unknowns x and y.
Solve it by any method (Substitution, Elimination, Determinant).
(2)
is equivalent to
x*ln(2) + y*ln(3) = (y-x)*ln(5), (1')
(x+y)*ln(10) = ln(2). (2')
It is a system of two linear equations in two unknowns x and y.
Solve it by any method (Substitution, Elimination, Determinant).