Please help me solve this equation
1. Solve the following inequality for x:
3x²-8x > 3
3x²-8x-3 > 0
(x-3)(3x+1) > 0
Critical numbers are the zeroes of
the factors, 3, -1/3.
We graph the critical numbers on a number line.
Since the inequality symbols are > and not  ,
the critical numbers cannot be solutions, so we draw
open circles at each critical number.
-----------o--------------------o-----------
-2 -1
,
the critical numbers cannot be solutions, so we draw
open circles at each critical number.
-----------o--------------------o-----------
-2 -1  0 1 2 3 4 5
We test each interval.
We pick a test point on
0 1 2 3 4 5
We test each interval.
We pick a test point on 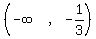 We pick -1 and substitute it in
(x-3)(3x+1) > 0
(-1-3)(3∙-1+1) > 0
(-4)(-3+1) > 0
(-4)(-2) > 0
8 > 0
That's true so we shade that interval on
the number line:
<==========o--------------------o-----------
-2 -1
We pick -1 and substitute it in
(x-3)(3x+1) > 0
(-1-3)(3∙-1+1) > 0
(-4)(-3+1) > 0
(-4)(-2) > 0
8 > 0
That's true so we shade that interval on
the number line:
<==========o--------------------o-----------
-2 -1  0 1 2 3 4 5
Show that it has two different rational roots.
Next we pick a test point on
0 1 2 3 4 5
Show that it has two different rational roots.
Next we pick a test point on 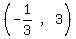 We pick 0 and substitute it in
(x-3)(3x+1) > 0
(0-3)(3∙0+1) > 0
(-3)(1) > 0
-3 > 0
That's false so we DO NOT shade that interval on
the number line. We still have this:
<==========o--------------------o-----------
-2 -1
We pick 0 and substitute it in
(x-3)(3x+1) > 0
(0-3)(3∙0+1) > 0
(-3)(1) > 0
-3 > 0
That's false so we DO NOT shade that interval on
the number line. We still have this:
<==========o--------------------o-----------
-2 -1  0 1 2 3 4 5
We test each interval.
We pick a test point on
0 1 2 3 4 5
We test each interval.
We pick a test point on 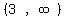 We pick 4 and substitute it in
(x-3)(3x+1) > 0
(4-3)(3∙4+1) > 0
(1)(12+1) > 0
(1)(13) > 0
13 > 0
That's true so we shade that interval on
the number line:
<==========o--------------------o==========>
-2 -1
We pick 4 and substitute it in
(x-3)(3x+1) > 0
(4-3)(3∙4+1) > 0
(1)(12+1) > 0
(1)(13) > 0
13 > 0
That's true so we shade that interval on
the number line:
<==========o--------------------o==========>
-2 -1  0 1 2 3 4 5
So the solution in interval notation is
0 1 2 3 4 5
So the solution in interval notation is
 ----------------
----------------
2. Without solving the equation 3x² - 8x - 3 = 0
Show that it has two different rational roots.
[That's funny for we already had to solve it to
get the critical values in the first problem. :) ]
But pretending we hadn't, we would just show that
the discriminant is a perfect square:
Discriminant = b²-4ac = (-8)²-4(3)(-3) = 64+36 = 100
which is 10², a perfect square, so we know that the
quadratic has two rational roots.
Edwin