Question 1042627: Given sinA=6/7 and cosB=-1/6, where Ais in quadrant II and B is in quadrant III, find sin(A+B), cos(A-B), and tan(A-b)
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Given sin(A) = 6/7 and cos(B) = -1/6, where A is in quadrant II and B is in quadrant III, find sin(A+B), cos(A-B), and tan(A-b)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Similar problems were solved many times here.
See the lessons
- Calculating trigonometric functions of angles
- Advanced problems on calculating trigonometric functions of angles
in this site. Find appropriate samples for you there.
The instructions are as follows:
1. Knowing that sin(A) = 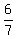 , calculate cos(A) = +/- , calculate cos(A) = +/- 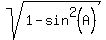 .
2. Knowing that the angle A is in QII, determine the sign at the square root in the n.1 above.
3. Knowing that cos(B) = .
2. Knowing that the angle A is in QII, determine the sign at the square root in the n.1 above.
3. Knowing that cos(B) = 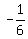 , calculate sin(B) = +/- , calculate sin(B) = +/-  .
4. Knowing that the angle B is in QIII, determine the sign at the square root in the n.3 above.
5. As a last step, apply the formulas
sin(A+B) = sin(A)*cos(B) + cos(A)*sin(B),
cos(A-B) = cos(A)*cos(B) + sin(A)*sin(B).
tan(A-B) = .
4. Knowing that the angle B is in QIII, determine the sign at the square root in the n.3 above.
5. As a last step, apply the formulas
sin(A+B) = sin(A)*cos(B) + cos(A)*sin(B),
cos(A-B) = cos(A)*cos(B) + sin(A)*sin(B).
tan(A-B) = 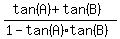 .
Notice that you just have everything to substitute into these formulas. .
Notice that you just have everything to substitute into these formulas.
See also the lessons
- Addition and subtraction formulas
- Addition and subtraction formulas - Examples
in this site.
|
|
|