.
Solve sin^2(theta) - 5cos(theta) = 5 for 0° <= theta < 360°.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Replace  by
by 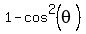 to have the equation for
to have the equation for  only. You will get
only. You will get
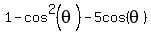 =
=  , or
, or
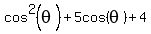 =
=  .
Factor left side:
.
Factor left side:
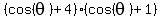 =
=  .
Then the equation deploys in two equations:
1)
.
Then the equation deploys in two equations:
1) 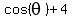 =
=  , or
, or  =
=  , which has no solutions, and
2)
, which has no solutions, and
2)  =
=  , or
, or  =
=  , which has the solution
, which has the solution  = 180°.
Answer. The solution is
= 180°.
Answer. The solution is  = 180°.
= 180°.