Question 1042421: Eighteen points are equally spaced on a circle, from which you will choose a certain number at random. How many do you need to choose to guarantee that you will have the four corners of at least one rectangle?
Help is much appreciated, do you need to draw a diagram? Thanks.
Found 2 solutions by ikleyn, robertb:
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Eighteen points are equally spaced on a circle, from which you will choose a certain number at random.
How many do you need to choose to guarantee that you will have the four corners of at least one rectangle?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
You need to have 2 (two) pairs of diametrically opposite points. Two different pairs, I mean.
Among any of 10 of the given points, there are at least two (one pair) of diametrically opposite points
(Dirichlet's principle // pigeonhole principle).
If you randomly choose 10 =  points, you guarantee at least 1 pair of diametrically opposite points. points, you guarantee at least 1 pair of diametrically opposite points.
If you randomly choose 11 = 10 + 1 points, you guarantee one pair of diametrically opposite points;
and after removing/withdrawing these two points, still there are at least one pair of diametrically opposite points
among the remaining 9 = 11-2 points.
Answer. You need to choose 11 points randomly.
Answer by robertb(5830)   (Show Source): (Show Source):
You can put this solution on YOUR website! You need to choose 11 points to guarantee that you will have four corners of a rectangle.
To see this, the space between any two consecutive points would be  , and hence 10 consecutive points, which corresponds , and hence 10 consecutive points, which corresponds
to 9  spaces, would constitute an entire semi-circle, i.e., spaces, would constitute an entire semi-circle, i.e.,  . .
Name the points  , ,  , , 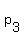 ,..., ,...,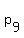 , , 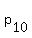
Now add an 11th consecutive point after 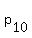 , and call it , and call it  . .
The segment with endpoints  and and 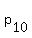 will be one diagonal of the rectangle, while the segment with endpoints will be one diagonal of the rectangle, while the segment with endpoints  and and 
will be the other diagonal of the rectangle formed.
|
|
|