.
Hi i have to solve this problem, thanks for help.
Sin^4x - Cos^4x = Sin^2x - Cos^2x
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Are you familiar with this identity: 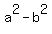 = {a+b)*(a-b)?
If not, or if you are not sure, look into the lesson The difference of squares formula in this site.
OK. Now, apply this identity to the left side. You will get
= {a+b)*(a-b)?
If not, or if you are not sure, look into the lesson The difference of squares formula in this site.
OK. Now, apply this identity to the left side. You will get
 =
= 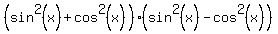 .
But the first parentheses,
.
But the first parentheses, 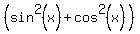 is equal to 1, as everybody knows.
Therefore,
is equal to 1, as everybody knows.
Therefore,
 =
=  .
QED.
.
QED.