Question 1042111: 1. In geometric sequence,the 2nd term is 2 and the 6th term is 2/81.Find the common ratio.
2.The sum of the first 5 terms of a geometric sequence is 93.If the 10th term is 3/2,find the common ratio and the 4th term of the sequence
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! In a geometric sequence:
 = the first term = the first term
 = the common ratio. = the common ratio.
Any other term or the sum of terms starting from  can be found from can be found from
 = the = the  term, and term, and
 = the sum of the first = the sum of the first  terms. terms.
1) The problem states that
 and and  . .
Was there any other information? Did it state that all the terms in the sequence were positive real numbers?
As posted, the problem has two solutions:
 ---> ---> ---> ---> . .
There are two real number solutions to  : :
either  or or  . .
If  , the sequence first term is , the sequence first term is  , and the next five terms are , and the next five terms are 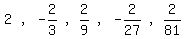 . .
If  , the sequence first term is , the sequence first term is  , and the next five terms are , and the next five terms are 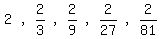 . .
2) The problem (as posted) states that
 and and  . .
From there, we get
 ---> ---> = = --->> --->> ---> ---> ---> ---> ---> ---> ---> --->
That last equation has no rational solution. It has only one real, irrational solution that can be approximated by  . .
It is easy to find such an approximate solution if you have a graphing calculator or the right computer software.
With that, we can calculate  from from
 : :
 ---> ---> ---> ---> (also an approximation), and (also an approximation), and
 (approximately). (approximately).
Did your instructor really epect you to solve the problem that way? Or is there a typo somewhere, so that there would be an easier, rational solution for  ? ?
|
|
|