SOLUTION: 3. Determine which of the following two rules (I or II) is an equivalent formulation of the recursive rule for Fibonacci numbers: I) FN- 1 - FN = FN +1 , N > 1 I

Algebra ->  Finance -> SOLUTION: 3. Determine which of the following two rules (I or II) is an equivalent formulation of the recursive rule for Fibonacci numbers: I) FN- 1 - FN = FN +1 , N > 1 I      Log On


   

Question 1041500: 3. Determine which of the following two rules (I or II) is an equivalent formulation of the recursive rule for Fibonacci numbers:
I) FN- 1 - FN = FN +1 , N > 1
II)FN +1 - FN = FN - 1 , N > 1
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
You needed some parentheses in there to keep what 
you wrote readable.  

So I will assume you meant this:

I) F(N-1) -   F(N)    =    F(N+1),  N > 1

II)F(N+1) -   F(N)    =    F(N-1),  N > 1

The Fibonacci recursion formula says

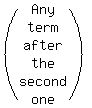
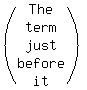
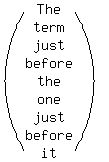
%28matrix%286%2C1%2C%0D%0AAny%2Cterm%2Cafter%2Cthe%2Csecond%2Cone%29%29%22%22=%22%22%28matrix%285%2C1%2C%0D%0AThe%2Cterm%2Cjust%2Cbefore%2Cit%29%29%22%22%2B%22%22%28matrix%289%2C1%2C%0D%0AThe%2Cterm%2Cjust%2Cbefore%2Cthe%2Cone%2Cjust%2Cbefore%2Cit%29%29

I) F(N-1) - F(N) = F(N+1)
F(N-1) is the term just before F(N), which is the term just
before F(N+1).

...,F(N-1),F(N),F(N+1),...

The correct formula should be F(N+1) = F(N-1) + F(N)

But that one (I) has a minus where it should be a plus.  So that one 
is wrong.

II)F(N+1) - F(N) = F(N-1), N > 1
This one is correct because if you solve for F(N+1),
by adding F(N) to both sides, you get:

             F(N+1) = F(N-1) + F(N)

Edwin