Question 1041173: the hypotenuse of a right triangle is 12 inches and the area is 24 square inches. Find the dimension of the triangle, correct to one decimal place.
Found 3 solutions by josgarithmetic, ikleyn, MathTherapy:
Answer by josgarithmetic(39617)   (Show Source): (Show Source):
Answer by ikleyn(52786)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The hypotenuse of a right triangle is 12 inches and the area is 24 square inches.
Find the dimension of the triangle, correct to one decimal place.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
 = =  , (1) , (1)
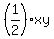 = =  , (2)
or , (2)
or
 = =  , (1') , (1')
 = =  . (2')
Multiply eqn. (2') by 2 and add to eqn(1') (both sides). You will get . (2')
Multiply eqn. (2') by 2 and add to eqn(1') (both sides). You will get
 = = 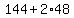 , or , or
 = =  , or , or
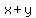 = = 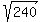 = = 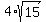 .
Thus from (1) and (2) we got
x + y = .
Thus from (1) and (2) we got
x + y = 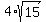 , (3)
xy = 48. (4)
Notice that in this way we decreased the degree of the original equations/system.
It makes it easier to work in future with (3),(4) instead of (1),(2).
Next, from (3) x = , (3)
xy = 48. (4)
Notice that in this way we decreased the degree of the original equations/system.
It makes it easier to work in future with (3),(4) instead of (1),(2).
Next, from (3) x = 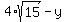 . Substitute it into (4) and get . Substitute it into (4) and get
 = =  . (5) . (5)
 = =  ,
Solve this quadratic equation by applying the quadratic formula. You will get ,
Solve this quadratic equation by applying the quadratic formula. You will get
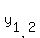 = = 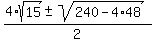 = = 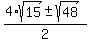 = =  .
Then .
Then  = =  - - 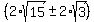 .
Answer. There are two solutions:
a) x = .
Answer. There are two solutions:
a) x = 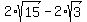 , y = , y = 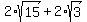 , and
b) x = , and
b) x = 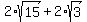 , y = , y = 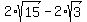 .
Check. a) .
Check. a) 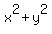 = =  = 144, xy = 4*15 - 4*3 = 60 - 12 = 48. OK ! ! ! = 144, xy = 4*15 - 4*3 = 60 - 12 = 48. OK ! ! !
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! the hypotenuse of a right triangle is 12 inches and the area is 24 square inches. Find the dimension of the triangle, correct to one decimal place.
Height and base: 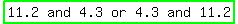
|
|
|