Question 1041012: Q: two line segment in the x y plane form a right triangle with the x axis,Having vertices (2,a),(0,0),(10,0).what is the area of triangle?
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Q: two line segment in the x y plane form a right triangle with the x axis, having vertices (2,a),(0,0),(10,0).
What is the area of triangle?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
It is clear that the vertex (2,a) is the right angle vertex and the segment [(0,0 - (10,0)] is the hypotenuse.
Then you can write the Pythagorean equation in the form
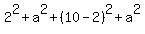 = = 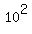 . (1)
It is your equation to find the unknown value of "a".
Simplify and solve it: . (1)
It is your equation to find the unknown value of "a".
Simplify and solve it:
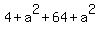 = =  , ,
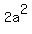 = = 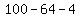 , ,
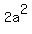 = =  ---> --->  = =  ---> a = 4.
Now, the hypotenuse has the length 10, while the altitude drawn to the hypotenuse has the length 4.
Hence, the area of the triangle is ---> a = 4.
Now, the hypotenuse has the length 10, while the altitude drawn to the hypotenuse has the length 4.
Hence, the area of the triangle is 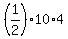 = 20 square units.
Answer. The area of the triangle is 20 square units. = 20 square units.
Answer. The area of the triangle is 20 square units.
Comment from student: can you tell me how you made this equation.
My response:
Let A be the point (0,0) in the coordinate plane (the origin);
let B be the point (2,a), and let C be the point (10,0).
Then the triangle ABC is right-angled triangle, according to the condition.
with the vertex B as the right angle and the segment AC as the hypotenuse.
Next, draw the perpendicular from the vertex B to the hypotenuse AC. The foot of this perpendicular is the point D = (2,0).
I recommend you to make a sketch of the triangle ABC and draw this perpendicular CD.
Now you have two right angled triangles, ADB and CDB.
From the triangle ADB you have  = = 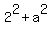 .
From the triangle CDB you have .
From the triangle CDB you have 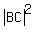 = = 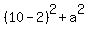 .
The equation (1) in my very first post is .
The equation (1) in my very first post is
 + + 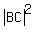 = = 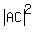 .
Everything is so obvious . . . .
Everything is so obvious . . .
I have a contr-question to you.
Why, when sending your question, you didn't mention the ID number of the problem?
|
|
|