Question 1040671: in triangle ABC right angled at B. BN perpendicular to AC, AC = 45 cm, BN = 5 cm find AB
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! in triangle ABC right angled at B.
BN perpendicular to AC, AC = 45 cm,
BN = 5 cm
find AB
draw and label the sides
a = side opposite angle A
b = side opposite angle B given as 45 cm (hypotenuse)
c = Side opposite angle C
label point N on AC, very close to A, draw a perpendicular to B
Then
a^2 + c^2 = 45^2
a^2 + c^2 = 2025
:
NB perpendicular to side b given as 5 cm, forms two smaller right triangles
which we can solve
let let x = NC
then
(45-x) = NA
therefore
c^2 = 5^2 + (45-x)^2
FOIL
c^2 = 25 + (2025 - 90x + x^2)
c^2 = x^2 - 90x + 2050
and
a^2 = 5^2 + x^2
a^2 = x^2 + 25
:
c^2 + a^2 = b^2
Substitute for c^2, a^2, and b^2 find x
(x^2 -90x + 2050) + (x^2+25) = 45^2
combine like terms
x^2 + x^2 - 90x + 2050 + 25 = 2025
2x^2 - 90x + 2075 - 2025 = 0
A quadratic equation
2x^2 - 90x + 50 = 0
using the quadratic formula a=2; b=-90; c= 50, I got
x = .5626
and
x = 44.4374 cm, the reasonable answer
then
45 - 44.4374 =.5626, we can use this to find c (which is AB)
c^2 = 5^2 + x^2
c^2 = 25 + .5626^2
c = 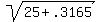
c = 5.032 cm is side AB
|
|
|