Question 1040466: LAST PROBLEM!!!!!!!!!!!!!!!!!!!
2. Find the following, rounded to two decimal places.
Y=X4^(x)
(a) the intervals on which the function is increasing or decreasing.
(b) the range of the function
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part A)
y = x*4^x
dy/dx = 4^x+x*ln(4)*4^x ... apply derivative; use product rule and log rule
dy/dx = 4^x * [ 1+x*ln(4) ] ... factor
Set dy/dx equal to zero. Then solve for x
4^x * [ 1+x*ln(4) ] = 0
4^x = 0 or 1+x*ln(4) = 0
4^x = 0 has no solutions
let's solve 1+x*ln(4) = 0
1+x*ln(4) = 0
x*ln(4) = -1
x = -1/ln(4)
x = -0.72134752044449
So dy/dx is only equal to zero when x = -0.72134752044449
If x is some smaller value, say x = -1, then
dy/dx = 4^x * [ 1+x*ln(4) ]
dy/dx = 4^(-1) * [ 1+(-1)*ln(4) ]
dy/dx = -0.09657359027998
So dy/dx is negative for x values such that x < -0.72134752044449
This means the original function is decreasing when x < -0.72134752044449. So on the interval (-infinity, -0.72134752044449)
Rounding to two decimal places gives (-infinity, -0.72)
Let's plug in a value to the right of -0.72134752044449, say x = 0
dy/dx = 4^x * [ 1+x*ln(4) ]
dy/dx = 4^(0) * [ 1+(0)*ln(4) ]
dy/dx = 1
telling us that f(x) is increasing on the interval (-0.72134752044449, infinity)
Rounding to two decimal places gives (-0.72, infinity)
To wrap up part a) we found that...
f(x) is decreasing on the interval (-infinity, -0.72)
f(x) is increasing on the interval (-0.72, infinity)
I'm using interval notation
--------------------------------------------------------------------
Part B)
In part A),we found that the function is decreasing on the interval from -infinity to -0.72134752044449. Then the function increases back again on the interval from -0.72134752044449 to infinity.
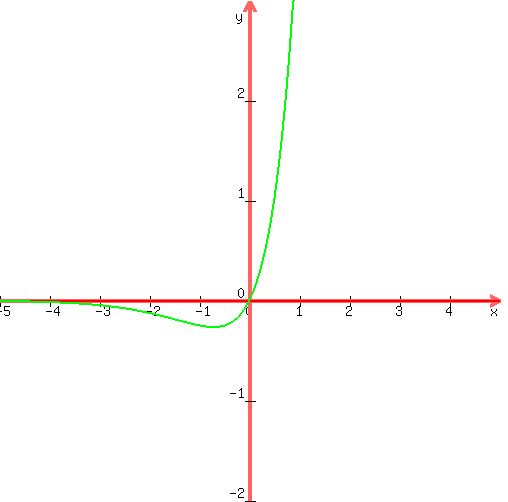
The graph will head downhill until it reaches x = -0.72134752044449. Then it will head back uphill. The question is: what is the corresponding y value for x = -0.72134752044449 ?
Let's find out by plugging in x = -0.72134752044449
y = x*4^x
y = -0.72134752044449*4^(-0.72134752044449)
y = -0.26536892271152
y = -0.27 ... rounding to two decimal places
The smallest y can get is -0.27
Therefore, the range in interval notation is [-0.27, infinity)
Take note how I used a square bracket to include the endpoint.
Here is a graph
|
|
|