Question 1040425: QUESTION 2:
A gas station sells three types of gas: Regular for $2.85 a gallon, Performance Plus for $3.10 a gallon, and Premium for $3.35 a gallon.
On a particular day 4000 gallons of gas were sold for a total of $12,125. Two times as many gallons of Regular as Premium gas were sold. How many gallons of each type of gas were sold that day?
I came up with the following system:
x+y+z=4000
2.85x+3.10y+3.35z=12125
x=2x
I tried using matrices but the answers I get do not work when plugged back into the system. These problems confuse the heck out of me!
THANK YOU!!!!!!
Found 2 solutions by ikleyn, MathTherapy:
Answer by ikleyn(52798)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
QUESTION 2:
A gas station sells three types of gas: Regular for $2.85 a gallon, Performance Plus for $3.10 a gallon, and Premium for $3.35 a gallon.
On a particular day 4000 gallons of gas were sold for a total of $12,125.
Two times as many gallons of Regular as Premium gas were sold. How many gallons of each type of gas were sold that day?
I came up with the following system:
x+y+z=4000
2.85x+3.10y+3.35z=12125
x=2x
I tried using matrices but the answers I get do not work when plugged back into the system. These problems confuse the heck out of me!
THANK YOU!!!!!!
~~~~~~~~~~~~~~~~~~~~~~~~~
The equation x = 2x is incorrect. It should be x = 2z.
So your system is
x + y + z = 4000, (1)
2.85x + 3.10y + 3.35z = 12125, (2)
x = 2z. (3)
or
x + y + x/2 = 4000, (1')
2.85x + 3.10y + 3.35*(x/2) = 12125 (2')
(no "z". "z" is just excluded). Multiply (1') and (2') by 2 (both sides) and collect the like terms.
3x + 2y = 8000, (3)
9.05x + 6.20y = 24250. (4)
I just did enough for you :=).
Can you complete on your own from this point?
Apply the substitution method. Express x from (3) an then substitute into (4). Good luck !
Let me know if you still have problems.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! QUESTION 2:
A gas station sells three types of gas: Regular for $2.85 a gallon, Performance Plus for $3.10 a gallon, and Premium for $3.35 a gallon.
On a particular day 4000 gallons of gas were sold for a total of $12,125. Two times as many gallons of Regular as Premium gas were sold. How many gallons of each type of gas were sold that day?
I came up with the following system:
x+y+z=4000
2.85x+3.10y+3.35z=12125
x=2x
I tried using matrices but the answers I get do not work when plugged back into the system. These problems confuse the heck out of me!
THANK YOU!!!!!!
Let amount of regular, performance plus, and premium sold, be R, Q, and P, respectively
Then equation for amount sold = R + Q + P = 4,000 ----- eq (i)
Equation for sales: 2.85R + 3.1Q + 3.35P = 12,125 ------ eq (ii)
Also, R = 2P ------ eq (iii)
2P + Q + P = 4,000 ------ Substituting 2P for R in eq (i)
3P + Q = 4,000______Q = 4,000 - 3P ------- eq (iv)
2.85(2P) + 3.1Q + 3.35P = 12,125 ------ Substituting 2P for R in eq (ii)
5.7P + 3.1Q + 3.35P = 12,125
9.05P + 3.1Q = 12,125 ------- eq (v)
9.05P + 3.1(4,000 - 3P) = 12,125 ----- Substituting 4,000 - 3P for Q in eq (v)
9.05P + 12,400 - 9.3P = 12,125
9.05P - 9.3P = 12,125 - 12,400
- .25P = - 275
P, or amount of premium gas sold = 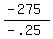 , or , or 
R = 2(1,100) ------- Substituting 1,100 for P in eq (iii)
R, or amount of regular gas sold = 
Q = 4,000 - 3(1,100) ------- Substituting 1,100 for P in eq (iv)
Q = 4,000 - 3,300
Q, or amount of performance plus gas sold = 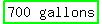
|
|
|