SOLUTION: A body is projected downward at an angle of 30 tp the horizontal with a velocity of 9.8m/s ftom the top of the tower of 29.4m high .how long will it take before striking the ground

The body moves uniformly at the constant speed in horizontal direction and at the constant acceleration 
g = 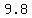  downward in vertical direction.
     (! Do not miss the initial velocity 9.8  with the gravity acceleration g =   !)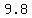

To answer the question, it is enough to consider vertical movement of the body.

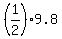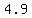
Its initial vertical velocity is  v =  =  =   directed downward.

Then an equation for the vertical coordinate of the body h(t) is

h(t) = ,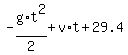

where g = 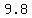   and  v = 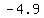 ,  or

h(t) = .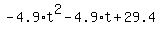

Here h(t) is the vertical distance from the body to the ground level in meters, t is time in seconds.

To find the time moment when the body strikes the ground, you need to solve a quadratic equation 

h(t) = 0,  or   = .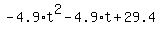

It is the same as 

 = . 

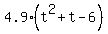The last equation is equivalent to 

 = .

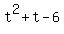Factor it. It is equivalent to

(t-3)*(t+2) = 0

and has the roots t = 3 and t = -2.

Only positive root is acceptable.

So, the answer is: t = 3.  The body hits the ground in 3 seconds.