SOLUTION: A machine is now worth $120,000 and will depreciate linearly over an 8-year period at which time it will be worth $25,000 as scrap. What will the machine be worth in 6 years?

Here is a graph to explain what you're being asked.
The word "linearly" tells us that a line is involved.

 

The point (0,$120000) represents the fact that when no (zero)
years have passed, that is, when the machine is brand new,
the machine is worth $120000.

The point (8,$25000) represents the fact that when 8 years have
passed, the machine is to be scrapped, the machine is worth 
$25000 as scrap.

You are being asked to find the value $????? of the machine after
6 years have passed.

So x = the number of years
And y = how much the machine is worth in x years.

That means we need to find the equation of the line
above that goes through the points (x1,y1) = (0,120000) and
the point (x2,y2) = (8,25000)

We use the slope formula to find the slope m:



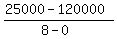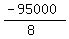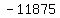Now we have the slope m = -11875.

We know that the equation of a line is

y = mx + b

where m = -11875 and since the y-intercept is (0,b) = (0,120000),
we can substitute m = -11875 and b = 120000 in y = mx + b
and we will have the equation of the above line.

So all you'll have to do to find what the machine is worth
after 6 years is to substitute x = 6 in the equation you'll
find for the above line.

Edwin