We wish to prove:
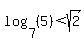 To get a motivation for how to prove it,
we first assume it true, (although that's
a far cry from knowing it is true!). Then
we see if that (unnecessarily true)
assumption leads to something we know is
true, then we see if we can reverse the
process by beginning with what we ended
up knowing is true.
Since we know that
To get a motivation for how to prove it,
we first assume it true, (although that's
a far cry from knowing it is true!). Then
we see if that (unnecessarily true)
assumption leads to something we know is
true, then we see if we can reverse the
process by beginning with what we ended
up knowing is true.
Since we know that  Then the proposition would be true if we
could prove that
Then the proposition would be true if we
could prove that
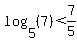 Let's seek a motivation for proving it by
(unjustifiably) assuming it true.
Since exponentiation to a positive power is
strictly increasing, we raise 5 to both sides
power:
Let's seek a motivation for proving it by
(unjustifiably) assuming it true.
Since exponentiation to a positive power is
strictly increasing, we raise 5 to both sides
power:
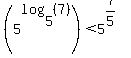 Simplifying
Simplifying
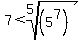
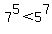
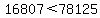 We know that is true, so let's begin the
proof starting with that and reversing
steps:
We begin with
We know that is true, so let's begin the
proof starting with that and reversing
steps:
We begin with
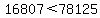
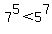 fifth root of positive numbers is an increasing function
So we take fifth roots of both sides:
fifth root of positive numbers is an increasing function
So we take fifth roots of both sides:
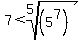 We rewrite both sides as powers of 5
We rewrite both sides as powers of 5
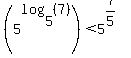 Since powers of 5 is a strictly increasing function,
the exponents are also strictly increasing.
Since powers of 5 is a strictly increasing function,
the exponents are also strictly increasing.
 And since
And since  ,
,
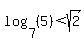 Edwin
Edwin