SOLUTION: If 2tanA + cot A =tanB then prove that 2 tan (B-A) =cot A

  
Quite often in mathematical proofs, we first do a 
"motivation search" for how to prove something 
by wrongly (yes wrongly!) and unjustifiably 
(yes unjustifiably!): 

1. assuming what we want to prove is true, 
2. reaching something we know is true, and then 
3. seeing if we can start with what we found
   to be true, and
4. reverse the steps of our 'wrong and unjustifiable' 
   trick to create a "correct and justifiable' proof. 

So let's first do a 'motivation search' by 'unjustifiably'
assuming what we want to prove. That is we assume this: 



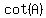Using well known identities:





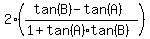
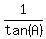
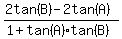
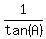Cross-multiply:





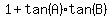
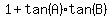Subtract tan(A)tan(B) from both sides:



Add 2tan²(A) to both sides:

(1)   

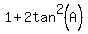Now let's use the given equation: 



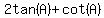
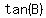Replacing the cot(A),

              

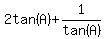
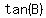and substitute for tan(B) in equation (1) above:

 

 

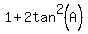
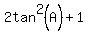
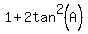Now we have reached an equation which we know is 
true.  But please realize that we haven't proved 
anything at all! We haven't even begun to prove 
anything! So now we start our proof by reversing 
our steps.

-------------------------------------

We know this is true:

 

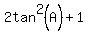
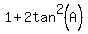On the left, break up tan2(A) as tan(A)tan(A)



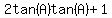
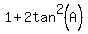Factor out tan(A) on the left

 

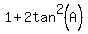Replace  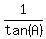by cot(A)

 

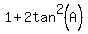We are given that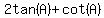 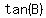, so
we can replace what's in the parentheses by tan(B)

  

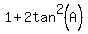Subtract 2tan²(A) from both sides:

 

Add tan(A)tan(B) to both sides:

 

 

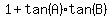
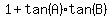Factor out 2tan(A) on the left:

 

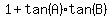Divide both sides by 1+tan(A)tan(B)

 

Divide both sides by tan(A)

 

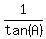Replace the expression in parentheses by tan(B-A) on left,
Replace 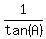 by cot(A) on the right:

 

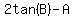
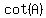Notice that we would never have guessed what true equation
we should start with and what manipulations to do with it 
if we hadn't begun by 'wrongly' assuming what we wanted to 
prove.  This is a technique useful for many proofs.

Edwin