Question 103975This question is from textbook Beginning Algebra
: Find all positive values for k for which each of the following can be factored.
x^2 + x - k
I know that normally we would find the factors of the co-efficient, but here, the co-efficient has no value other than one. Does this mean that this cannot be factored?
This question is from textbook Beginning Algebra
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website! First list all possible values that add to 1 (which is the coefficient of x):
2+-1=1,
3+-2=1,
4+-3=1,...
Notice the pattern? This pattern is generalized to
n+-(n-1)=n+-n+1=1
This means n and -(n-1) add to 1
So if we multiply n and -(n-1), we get
So this means  where n is any integer.
So for the first 10 values, we get:
If n=2, then k=-2 which can be factored into  .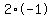
If n=3, then k=-6 which can be factored into  .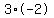
If n=4, then k=-12 which can be factored into  .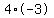
If n=5, then k=-20 which can be factored into  .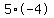
If n=6, then k=-30 which can be factored into  .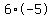
If n=7, then k=-42 which can be factored into  .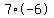
If n=8, then k=-56 which can be factored into  .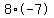
If n=9, then k=-72 which can be factored into  .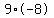
If n=10, then k=-90 which can be factored into  .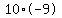
If n=11, then k=-110 which can be factored into  .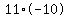
If n=12, then k=-132 which can be factored into  .
This list goes on...
|
|
|
