Question 1039430: In a town 85% of the people speak English, 40% speak kannada
and 20% speak Hindi, also 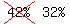 speak English and Kannada, speak English and Kannada,
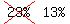 speak kannada and Hindi. And 10% speak English and Hindi. speak kannada and Hindi. And 10% speak English and Hindi.
Find the percentage of people who can speak all the three languages?
Found 4 solutions by Edwin McCravy, solver91311, ikleyn, AnlytcPhil:
Answer by Edwin McCravy(20065)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Sorry, this has no solution. One or more of the numbers
you have posted above is incorrect. Check the source
for which you copied the problem carefully. You may state
the corrected problem in the thank-you note form below,
and I'll get back to you by email.
Edwin
Answer by solver91311(24713)   (Show Source): (Show Source):
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a town 85% of the people speak English, 40% speak kannada and 20% speak Hindi, also 42% speak English and Kannada,
23% speak kannada and Hindi. And 10% speak English and Hindi. Find the percentage of people who can speak all the three languages?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
The input data is wrong.
For example, more people speak English and Kannada (42%) than kannada (40%) - absurd.
Answer by AnlytcPhil(1810)   (Show Source): (Show Source):
You can put this solution on YOUR website!
I think I know exactly what the mistakes are! The 42% should
be 32% and the 23% should be 13%.
In a town 85% of the people speak English, 40% speak kannada
and 20% speak Hindi, also 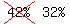 speak English and Kannada, speak English and Kannada,
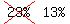 speak kannada and Hindi. And 10% speak English and Hindi. speak kannada and Hindi. And 10% speak English and Hindi.
Find the percentage of people who can speak all the three languages?
 Everybody in circle E speaks English.
Everybody in circle K speaks Kannada.
Everybody in circle H speaks Hindi.
If the little letters represent the percentages in
each of the 7 regions, then
p+q+r+s+t+u+v = 100%. Let's not bother
with the percent marks:
p+q+r+s+t+u+v = 100
Everybody in circle E speaks English.
Everybody in circle K speaks Kannada.
Everybody in circle H speaks Hindi.
If the little letters represent the percentages in
each of the 7 regions, then
p+q+r+s+t+u+v = 100%. Let's not bother
with the percent marks:
p+q+r+s+t+u+v = 100
In a town 85% of the people speak English,
p+q+s+t = 85
40% speak kannada
q+r+t+u = 40
and 20% speak Hindi,
s+t+u+v = 20
also 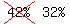 speak English and Kannada, speak English and Kannada,
q+t = 32
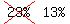 speak kannada and Hindi. speak kannada and Hindi.
t+u = 13
And 10% speak English and Hindi.
s+t = 10
Find the percentage of people who can speak all the three languages?
So we want the value of t.
The 7 equations in 7 unknowns are
1. p+q+r+s+t+u+v = 100
2. p+q+ s+t = 85
3. q+r +t+u = 40
4. s+t+u+v = 20
5. q +t = 32
6. t+u = 13
7. s+t = 10
Let's get all the other 6 letters
in terms of t:
From 7,
8. s = 10-t
From 5,
9. q = 32-t
From 2,
p+32-t+10-t+t = 85
p-t+42 = 85
10. p = 43+t
From 6,
11. u = 13-t
8. s = 10-t
From 4,
10-t+t+13-t+v = 20
23-t+v = 20
12. v = t-3
9. q = 32-t
11. u = 13-t
From 3,
32-t+r+t+13-t = 40
r-t+45 = 40
13. r = t-5
Now that we have all the other 6 letters in terms of t,
we can substitute into 1:
1. p+q+r+s+t+u+v = 100
43+t+32-t+t-5+10-t+t+13-t+t-3 = 100
90+t = 100
t = 10
That's the answer. But let's fill in the Venn diagram:
p = 43+t = 43+10 = 53
q = 32-t = 32-10 = 22
r = t-5 = 10-5 = 5
s = 10-t = 10-10 = 0
t = 10
u = 13-t = 3
v = t-3 = 10-3 = 7
So the Venn diagram is:
 Edwin
Edwin
|
|
|