|
Question 1039403: A and B can do a work in 12 days,B and C in 16 days. A started work and afte 7 days he stopd work and B started the work,after 5days B stopd work and remaining work was completed by C in 13days. In how many days A ,B,C alone can finish the work.
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
You can put this solution on YOUR website! a, b, c, the times in days for A, B, and C to do "one whole work". Use the work rates as 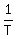 in unit of in unit of  . .

A sequence of workers has done one whole job.

Goal is to solve for a, b, and c.
Use the first two equations to solve each in terms of b.
-



-



-
Substitute these into the Finished In Thirteen Days equation.
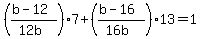
Simplify.
 , and simplest denominator IS 2*2*2*2*3*b; , and simplest denominator IS 2*2*2*2*3*b;







 ------------Seems strange, maybe correct, but needs to be rechecked ... Maybe a mistake was made. If you can understand the process up to here, your work MIGHT be better and without any mistake I made. You could then continue to go back to the first two equations to solve for a and c. ------------Seems strange, maybe correct, but needs to be rechecked ... Maybe a mistake was made. If you can understand the process up to here, your work MIGHT be better and without any mistake I made. You could then continue to go back to the first two equations to solve for a and c.
|
|
|
| |