.
Find all solutions of the equation in the interval [0, 2pi).
Sec^2x - secx = 2
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
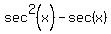 =
=  .
Introduce new variable u = seq(x). Then your equation becomes
.
Introduce new variable u = seq(x). Then your equation becomes
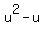 =
=  ,
,
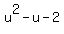 =
=  .
Factor the left side. You will get
(u-2)*(u+1) = 0.
The solutions are
u = 2 and/or u = -1.
From this point you have two equations:
1) sec(x) = 2 --->
.
Factor the left side. You will get
(u-2)*(u+1) = 0.
The solutions are
u = 2 and/or u = -1.
From this point you have two equations:
1) sec(x) = 2 ---> 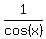 = 2 ---> cos(x) =
= 2 ---> cos(x) =  ---> x = +/-
---> x = +/- +
+  , k = 0, +/-1, +/-2, . . . and
2) sec(x) = -1 --->
, k = 0, +/-1, +/-2, . . . and
2) sec(x) = -1 ---> 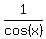 = -1 ---> cos(x) =
= -1 ---> cos(x) =  ---> x =
---> x =  +
+  , k = 0, +/-1, +/-2, . . .
Answer. x = +/-
, k = 0, +/-1, +/-2, . . .
Answer. x = +/- +
+  , k = 0, +/-1, +/-2, . . . and
x =
, k = 0, +/-1, +/-2, . . . and
x = 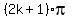 , k = 0, +/-1, +/-2, . . .
, k = 0, +/-1, +/-2, . . .
Solved.