SOLUTION: A (4,0) B (0,8) C (7,4). A point N lies on AB as such so that CN is perpendicular to AB. Find the coordinates of N. So, I found that the gradient of AB is -2 so that the gradien

Click here to see ALL problems on Length-and-distance

Question 1037852: A (4,0) B (0,8) C (7,4). A point N lies on AB as such so that CN is perpendicular to AB. Find the coordinates of N.
So, I found that the gradient of AB is -2 so that the gradient of CN has to be 1/2, right? But how do you find N from that?
Found 4 solutions by josgarithmetic, stanbon, josmiceli, MathTherapy:
Answer by josgarithmetic(39630)   (Show Source):
You can put this solution on YOUR website!
Slope of AB is ; and you have a point C(7,4) which must be on the line PERPENDICULAR to line AB.

Any line in the plane perpendicular to line AB will have slope .
.

You are looking for the equation of the line with slope and containing point (7,4). Use the point-slope form equation.
.
BUT WHAT IS POINT N?

Two lines intersect at some point. These will be perpendicular lines. You know one of them is , and the other is line AB. Finish finding the equation for line AB.
-
Choosing to use slope-intercept form,
------Line AB.

Point N is the intersection of and .
You find this point N.

Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website!
A (4,0) B (0,8) C (7,4). A point N lies on AB as such so that CN is perpendicular to AB. Find the coordinates of N.
So, I found that the gradient of AB is -2 so that the gradient of CN has to be 1/2, right? But how do you find N from that?
-----
Form of CN:: y = mx + b
---
Using C(7,4) and m = -2, solve for "b"::
4 = -2*7 + b
b = 18
---------
Equation of CN:: y = -2x + 18
-----------------------
Cheers,
Stan H.
------------------

Answer by josmiceli(19441)   (Show Source):
You can put this solution on YOUR website!
Slope of AB:

Any line perpendicular to this one
has slope

------------------
Use the general point-slope formula given the
point C(7,4) and the slope

(1)
---------------------
Likewise, the equation of line through AB is
A(4,0)
B(0,8)

(2)
-------------------
Multiply both sides of (1) by
and add (1) and (2)
(1)
(2)
-------------------

and
(2)
(2)
(2)
--------------------
So, the point N is:
N( 3,2 )
--------------------
Here's the plot of (1) and (2)
The answer looks right

Answer by MathTherapy(10557)   (Show Source):
You can put this solution on YOUR website!

A (4,0) B (0,8) C (7,4). A point N lies on AB as such so that CN is perpendicular to AB. Find the coordinates of N.
So, I found that the gradient of AB is -2 so that the gradient of CN has to be 1/2, right? But how do you find N from that?

You're correct up to that point! Good job!!
With line AB having a gradient (slope) of 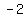, and point A (4, 0), we find that the equation of line AB is:
With line CN having a gradient (slope) of , and point C (7, 4), we find that the equation of line CN is:
Since line CN is PERPENDICULAR to line AB, it follows that these 2 lines intersect at N. Therefore, we set the equations equal
to each other and find (x, y). This gives us: . Solving this equation for x, then substituting the value of x
in any of the 2 equations will result in a value for y. These values (x, y) will be the coordinates of point N, and should be: