|
Question 1037844: Can someone please help my daughter with this problem and show her step-by-step how to do it her geometry class is a SE class as she has a learning problem in math that is why she has been asking to be shown step by step how to do the problem if she sees how it is done she understands it better the problem states find the perimeter of quadrilateral STUV, S(-5,-3) T(7,-2) U(7,-6) V(-5,-6)
Found 3 solutions by stanbon, Edwin McCravy, Alan3354:
Answer by stanbon(75887)   (Show Source):
You can put this solution on YOUR website! find the perimeter of quadrilateral STUV, S(-5,-3) T(7,-2) U(7,-6) V(-5,-6)
-----
The quadrilateral has 4 sides:: ST ; TU ; UV ; VS
-------
Find the length of each of the sides::
ST = sqrt[(-2+3)^2 + (7+5)^2] = sqrt[1 + 144] = sqrt(145)=
----
TU = sqrt[(-6+2)^2+(7-7)^2] sqrt[16+0] = sqrt(16) = 4
-------
UV = sqrt[(-6+6)^2+(-5-7)^2] = sqrt[0+144] = 12
----------
VS = sqrt[(-6+3)^2 + (-5+5)^2] = sqrt[9+0] = 3
-----------
Perimeter = 3 + 12 + 4 + sqrt(145) = 19+sqrt(145)
-------------
Cheers,
Stan H.
-------------
Answer by Edwin McCravy(20056)  (Show Source):
You can put this solution on YOUR website! quadrilateral STUV, S(-5,3) T(7,-2) U(7,-6) V(-5,-6)
The perimeter is just how many units it is all the way around
the quadrilateral. You can get 3 of the sides just by counting
the blocks on the graph paper.
From S to V is 9 units straight down.
From V to U is 12 units left to right.
From U to T is 4 units straight up.
The only line that we have to calculate is the slanted one from S to T.
We do that by drawing a horizontal line from T over to the line SV, like
below. We will label the point W(-5,-2) where it intersects line SV:
To calculate to upper side ST of the quadrilateral, we use the
Pythagorean theorem on right triangle SWT, which states that
  
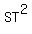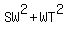We count blocks and get that WT = 12, the same as VU. And we
see that SW is 5 unit long, by counting blocks.
So we substitute 12 for SW and 5 for WT
 
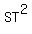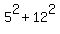
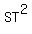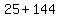
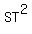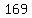
From the calculator we can get that square
root to be 13.
Then the perimeter is the sum of all four
sides:
SV + VU + UT + ST = 9 + 12 + 4 + 13 = 38
So the perimeter is 38.
Edwin
Answer by Alan3354(69443)  (Show Source):
You can put this solution on YOUR website! That's not the same problem that was posted earlier. There's a change of sign on one of the points.
====================
As I said earlier: show what you did. If you know the answer, post that.
|
|
|
| |
