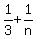SOLUTION: How many positive integers {{{ n }}} less than 2015 have the property that {{{ 1/3 + 1/n }}} can be simplified to a fraction with denominator less than {{{ n }}}?

 = 

Certainly the denominator 3n is greater than n.  Therefore
the fraction must reduce.  Thus let d > 1 be the greatest
common divisor of n+3 and 3n, the numerator and denominator.

Then there exist positive integers k,m such that

n+3 = kd and 3n = md

So the fraction  reduces to 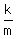, where m < n.

Then n = kd-3, and by substitution

3(kd-3) = md
3kd - 9 = md
 3kd-md = 9
d(3k-m) = 9
      d =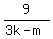 

So 3k-m is a divisor of 9, either 1, 3, or 9.

Since d > 1, 3k-m ≠ 9. So d is one of the
other two possibilities, d=3 or d=9

If d=3, then 3k-m = 3
   3k = m+3
    k =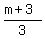 

Since n+3 = kd,
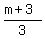n+3 = *3
n+3 = m+3
  n = m

But that contradicts m < n

So d=9, and 3k-m = 1
m = 3k-1
3n = md = dm
3n = 9(3k-1)
 n = 3(3k-1)
 n = 9k-3

Therefore n must be in the sequence 6,15,24,...,9k-3,...

n = 9k-3 ≤ 2015
      9k ≤ 2018
       k ≤ 224.2222...

So maximum value of k is 224,
thus the answer is 224.

Edwin